Dinamik ile İlgili Problem

Üniversite Makine Mühendisliği
1

Ekran görüntüsü 2025-01-16 000655
Ekran görüntüsü 2025-01-16 000655867×234 18.1 KB

2

Dinamik ile İlgili Problem

Çözüm:

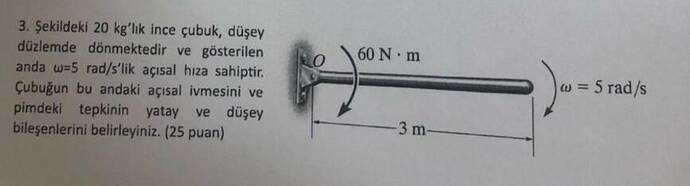
Bu problemde verilmiş olan bilgilerden yola çıkarak, ince çubuğun açısal ivmesini ve pimdeki tepkilerin yatay ve düşey bileşenlerini hesaplayacağız.

Adım 1: Verilerin Belirlenmesi

  • İnce çubuğun kütlesi: m = 20 \, \text{kg}
  • Çubuğun uzunluğu: L = 3 \, \text{m}
  • Açısal hız: \omega = 5 \, \text{rad/s}
  • Uygulanan tork: M = 60 \, \text{N} \cdot \text{m}

Adım 2: Açısal İvmenin Hesaplanması

  1. Eylemsizlik Momenti ( I ):

    İnce çubuğun eylemsizlik momenti, dönme ekseni ( O )'dan geçtiği için:

    I = \frac{1}{3} m L^2

    Buradan,

    I = \frac{1}{3} \times 20 \, \text{kg} \times (3 \, \text{m})^2 = 60 \, \text{kg} \cdot \text{m}^2

  2. Açısal İvme ( \alpha ):

    Tork eşitliğini kullanarak:

    M = I \cdot \alpha

    Buradan,

    60 \, \text{N} \cdot \text{m} = 60 \, \text{kg} \cdot \text{m}^2 \cdot \alpha
    \alpha = 1 \, \text{rad/s}^2

Adım 3: Pim Tepkilerinin Hesaplanması

  1. Çubuğun Ağırlığı:

    ( G = mg = 20 , \text{kg} \times 9.81 , \text{m/s}^2 = 196.2 , \text{N} )

  2. Merkezkaç (Santrifüj) Kuvveti:

    Çubuğun dönme hareketi nedeniyle merkezkaç kuvveti,

    F_c = m \cdot \omega^2 \cdot \frac{L}{2} = 20 \, \text{kg} \times (5 \, \text{rad/s})^2 \times 1.5 \, \text{m} = 750 \, \text{N}

  3. Yatay Bileşen (Rx):

    Merkezkaç kuvvetinden dolayı:

    R_x = F_c = 750 \, \text{N}

  4. Düşey Bileşen (Ry):

    Newton’un ikinci yasasına göre:

    R_y + G = m \cdot a_{\text{çubuğun ağırlık merkezi}} = m \cdot \frac{L}{2} \cdot \alpha

    Buradan:

    R_y = m \cdot \frac{L}{2} \cdot \alpha - G
    R_y = 20 \, \text{kg} \times 1.5 \, \text{m} \times 1 \, \text{rad/s}^2 - 196.2 \, \text{N} = 103.8 \, \text{N}

Sonuç:

  • Açısal ivme: \alpha = 1 \, \text{rad/s}^2
  • Pim tepkisinin yatay bileşeni: R_x = 750 \, \text{N}
  • Pim tepkisinin düşey bileşeni: R_y = 103.8 \, \text{N}