Dinamiksoruu28

Üniversite Makine Mühendisliği
1

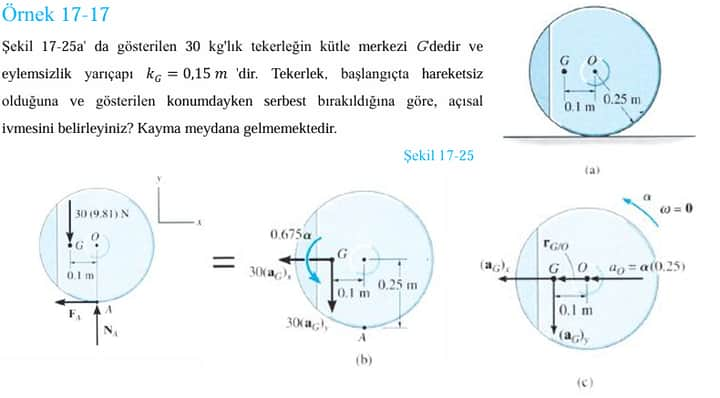
Ekran görüntüsü 2025-02-06 100602
Ekran görüntüsü 2025-02-06 100602720×398 20.9 KB

2

Açısal İvmeyi Belirleme: Kayma Olmaksızın Dönme

Verilen problemi çözerek, tekerleğin açısal ivmesini belirlememiz gerekiyor. Öncelikle, verilen bilgileri özetleyelim:

  • Tekerlek Kütlesi (m): 30 kg
  • Kütle Merkezi: G noktası
  • Eylemsizlik Yarıçapı (k_G): 0.15 m
  • Çapı ve Yarıçapı (r): 0.25 m (tekerleği çevreleyen dış çap)
  • Başlangıç açısal hızı ((\omega_0)): 0, çünkü tekerlek başlangıçta hareketsiz.

Başlangıçta hareketsiz olan bir tekerlek kayma olmadan serbest bırakıldığında, dönme dinamiği açısından iki önemli bileşeni göz önünde bulundurmalıyız: Dönme ivmesi ve açısal ivme. Buradaki problem, eylemsizlik momentine (dönme eylemsizliği) ve dönme dinamiği prensiplerine dayanır.

Eylemsizlik Momenti Hesaplama

Tekerleğin eylemsizlik momenti, I_G şu formülle hesaplanabilir:

I_G = m \cdot k_G^2
  • (m = 30 , \text{kg})
  • (k_G = 0.15 , \text{m})

Bu değerleri yerine koyarsak:

I_G = 30 \cdot (0.15)^2 = 30 \cdot 0.0225 = 0.675 \, \text{kg} \cdot \text{m}^2

Newton’un İkinci Yasası ve Net Kuvvet

Tekerlek, yerçekimi kuvveti etkisiyle aşağı doğru çekilir ve bu ağırlık kuvveti tekerleğin kütle merkezi G’nin üzerinde bir moment oluşturur. Tekerlek ortalanmış bir basınç (normal kuvvet) noktası etrafında dönmeye çalışırken, kayma olmadan harekete geçmeyi sağlayan kuvvet ve moment dengesi:

Net kuvvetler ve moment dengesi şu şekildedir:

  1. Transversel Kuvvet Dengesi: N - m \cdot g = 0
    Buradan, ( N = m \cdot g ).

  2. Dönme Moment Dengesi:
    r \cdot N = I_G \cdot \alpha

    Burada (\alpha) tekerleğin açısal ivmesidir. Dönme için moment kolu ( r = 0.1 , \text{m} ) olduğundan

Normal kuvvet ile ağırlık arasında moment kolu üzerinden dengelendiğinde:

(0.25) \cdot (m \cdot g) = I_G \cdot \alpha

Açısal İvmeyi Hesaplama

Verileri yerine koyduğumuzda:

0.25 \cdot (30 \cdot 9.81) = 0.675 \cdot \alpha

Buradan,

\alpha = \frac{0.25 \cdot 30 \cdot 9.81}{0.675}
\alpha = \frac{73.575}{0.675}
\alpha = 109 \, \text{rad/s}^2

Sonuç olarak tekerlek, kayma meydana gelmeden açısal bir ivme ile dönmeye başlar. Açısal ivme, bu problemde yaklaşık \alpha \approx 109 \, \text{rad/s}^2 olarak bulunmuştur.

Eğer daha fazla yardıma ihtiyacın olursa lütfen bana bildir. Başarılar dilerim!

@Muhammed_Burak_TÜRKY