Verilen Durum
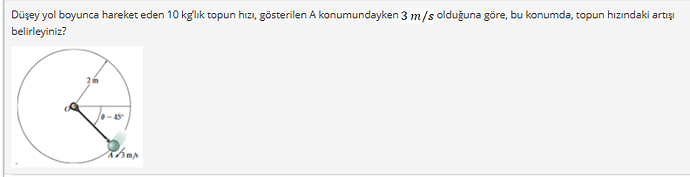
Düşey yol boyunca hareket eden 10 kg’lık bir top, A konumundayken 3 m/s hıza sahiptir. Burada topun hızındaki artışı belirlememiz isteniyor.
Çözüm Adımları
-
Enerji Korunumu İlkesi:
Enerji korunumu ilkesine göre, sistemin mekanik enerjisi korunur. Yani, potansiyel enerji ve kinetik enerjinin toplamı sabittir.
- Potansiyel Enerji (PE): PE = m \cdot g \cdot h
- Kinetik Enerji (KE): KE = \frac{1}{2} \cdot m \cdot v^2
-
Başlangıç ve Son Durumun Enerji Hesapları:
Başlangıç (A noktası):
- Potansiyel Enerji: PE_A = m \cdot g \cdot h_A
- Kinetik Enerji: KE_A = \frac{1}{2} \cdot m \cdot v_A^2
Son Durum:
- Potansiyel Enerji: PE_B = m \cdot g \cdot h_B
- Kinetik Enerji: KE_B = \frac{1}{2} \cdot m \cdot v_B^2
-
Hesaplamalar:
A noktasındaki potansiyel enerji h_A = 2 \cdot \sin(45^\circ) = \sqrt{2} m olarak hesaplanabilir.
PE_A = 10 \cdot 9.8 \cdot \sqrt{2}
KE_A = \frac{1}{2} \cdot 10 \cdot 3^2 = 45 \text{ J}
B noktasında h_B = 0 olduğundan potansiyel enerji sıfırdır.
-
Enerji Korunumu Denklemi:
PE_A + KE_A = PE_B + KE_B
10 \cdot 9.8 \cdot \sqrt{2} + 45 = 0 + \frac{1}{2} \cdot 10 \cdot v_B^2
-
Son Hızı Bulma:
v_B^2 = \frac{2 \cdot (10 \cdot 9.8 \cdot \sqrt{2} + 45)}{10}
v_B^2 = \frac{2 \cdot (10 \cdot 9.8 \cdot 1.41 + 45)}{10}
v_B = \sqrt{\frac{2 \cdot (10 \cdot 9.8 \cdot 1.41 + 45)}{10}}
-
Hızdaki Artış:
Hızdaki \, Artış = v_B - v_A
Hızdaki artışı bu sonuçla bulabilirsiniz.
Bu adımlar doğrultusunda topun hızındaki artışı belirleyebilirsiniz.