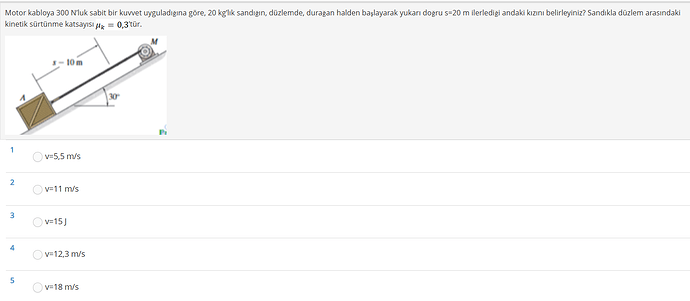
Görseldeki soruya bakalım ve hızı hesaplayalım.
Problem Analizi
Verilen:
- Motor, kabloya 300 N sabit kuvvet uyguluyor.
- Sandığın kütlesi 20 kg.
- Sandık durgun halden başlayarak 20 m yukarı doğru ilerliyor.
- Eğimin açısı (30^\circ).
- Kinetik sürtünme katsayısı (\mu_k = 0,3).
- Yerçekimi ivmesi (g = 9,8 , \text{m/s}^2).
Hız ((v)) bulunacak.
Çözüm Adımları
1. Kuvvetler
-
Çekme Kuvveti ((F_{\text{çekme}})): 300 N
-
Yerçekimi Kuvveti ((F_{\text{yerçekimi}})):
( F_{\text{yerçekimi}} = m \cdot g \cdot \sin(30^\circ) = 20 \cdot 9,8 \cdot 0,5 = 98 , \text{N} )
-
Kinetik Sürtünme Kuvveti ((F_{\text{sürtünme}})):
( F_{\text{sürtünme}} = \mu_k \cdot m \cdot g \cdot \cos(30^\circ) = 0,3 \cdot 20 \cdot 9,8 \cdot \sqrt{3}/2 \approx 50,95 , \text{N} )
2. Net Kuvvet ((F_{\text{net}}))
Net kuvvet:
[ F_{\text{net}} = F_{\text{çekme}} - F_{\text{yerçekimi}} - F_{\text{sürtünme}} = 300 - 98 - 50,95 \approx 151,05 , \text{N} ]
3. İvme ((a))
Newton’un 2. yasasına göre:
[ F_{\text{net}} = m \cdot a ]
[ a = \frac{F_{\text{net}}}{m} = \frac{151,05}{20} \approx 7,55 , \text{m/s}^2 ]
4. Hız ((v))
Kinematik denklem kullanarak, ilk hız 0 m/s iken son hız:
[ v^2 = u^2 + 2as ]
[ v^2 = 0 + 2 \cdot 7,55 \cdot 20 ]
[ v^2 = 302 ]
[ v \approx \sqrt{302} \approx 17,38 , \text{m/s} ]
Bu hesaplamalara göre, seçeneklerde en yakın hız 5) v = 18 , \text{m/s} olarak görünüyor. Dolayısıyla doğru cevap 5. seçenektir.