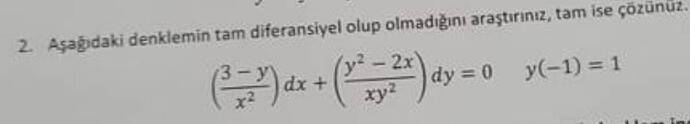Aşağıdaki denklemin tam diferansiyel olup olmadığını araştırınız, tam ise çözünüz.
\left(\frac{3 - y}{x^2}\right)dx + \left(\frac{y^2 - 2x}{xy^2}\right)dy = 0, \quad y(-1) = 1
Cevap:
1. Tam Diferansiyel Denklemi Kontrol Etme
Tam diferansiyel denklemler, genellikle şu formdadır:
M(x, y)dx + N(x, y)dy = 0
Verilen denklemi bu formata göre yeniden yazalım:
M(x, y) = \frac{3 - y}{x^2}
N(x, y) = \frac{y^2 - 2x}{xy^2}
Bir diferansiyel denklemin tam olması için gereken koşul şudur:
\frac{\partial M}{\partial y} = \frac{\partial N}{\partial x}
Öncelikle, M ve N ifadelerinin kısmi türevlerini hesaplayalım.
2. Kısmi Türevlerin Hesaplanması
\frac{\partial M}{\partial y} = \frac{\partial}{\partial y} \left(\frac{3 - y}{x^2}\right) = \frac{-1}{x^2}
\frac{\partial N}{\partial x} = \frac{\partial}{\partial x} \left(\frac{y^2 - 2x}{xy^2}\right)
Önce \frac{y^2 - 2x}{xy^2} ifadesini daha sade hale getirelim:
\frac{y^2 - 2x}{xy^2} = \frac{y^2}{xy^2} - \frac{2x}{xy^2} = \frac{1}{x} - \frac{2}{y^2}
Şimdi türevini alalım:
\frac{\partial}{\partial x} \left( \frac{1}{x} - \frac{2}{y^2} \right) = -\frac{1}{x^2}
3. Tam Diferansiyel Denklemi Kontrol Etme
Üstteki türevleri kıyaslayalım:
\frac{\partial M}{\partial y} = \frac{-1}{x^2}
\frac{\partial N}{\partial x} = -\frac{1}{x^2}
Görüldüğü gibi:
\frac{\partial M}{\partial y} = \frac{\partial N}{\partial x}
Dolayısıyla, bu diferansiyel denklemin tam diferansiyel olduğunu doğruladık.
4. Tam Diferansiyel Denklemin Çözülmesi
Bu aşamada çözümü yapabiliriz. Tam diferansiyel denklemin çözümü için bir potansiyel fonksiyon \psi(x, y) bulmamız gerekir, böylece:
\frac{\partial \psi}{\partial x} = M
\frac{\partial \psi}{\partial y} = N
Bu potansiyel fonksiyonu bulmak için önce M ile başlayalım:
\frac{\partial \psi}{\partial x} = \frac{3 - y}{x^2}
\psi'yi x'e göre integre edelim:
\psi(x,y) = \int \frac{3 - y}{x^2} \, dx = \int \left( 3x^{-2} - yx^{-2} \right) \, dx = \int 3x^{-2} \, dx - y \int x^{-2} \, dx
\psi(x,y) = 3 \left( -x^{-1} \right) - y \left( -x^{-1} \right)
\psi(x,y) = -\frac{3}{x} + \frac{y}{x} + h(y)
Şimdi, \psi'yi y'ye göre türevini alıp N'ye eşitleyelim:
\frac{\partial \psi}{\partial y} = \frac{1}{x} + \frac{dh(y)}{dy}
\frac{1}{x} + h'(y) = \frac{1}{x} - \frac{2}{y^2}
Buradan:
h'(y) = -\frac{2}{y^2}
h(y) = \int -\frac{2}{y^2} \, dy = 2y^{-1} + K
h(y) = \frac{2}{y} + K
Sonuçta \psi fonksiyonunu bulalım:
\psi(x, y) = -\frac{3}{x} + \frac{y}{x} + \frac{2}{y} + K
Genel çözüm için \psi(x, y) = C denklemini yazalım:
-\frac{3}{x} + \frac{y}{x} + \frac{2}{y} = C
Başlangıç koşulunu kullanarak C değerini bulalım: y(-1) = 1
-\frac{3}{-1} + \frac{1}{-1} + \frac{2}{1} = C
3 - 1 + 2 = C
C = 4
Sonuç olarak çözüm:
-\frac{3}{x} + \frac{y}{x} + \frac{2}{y} = 4