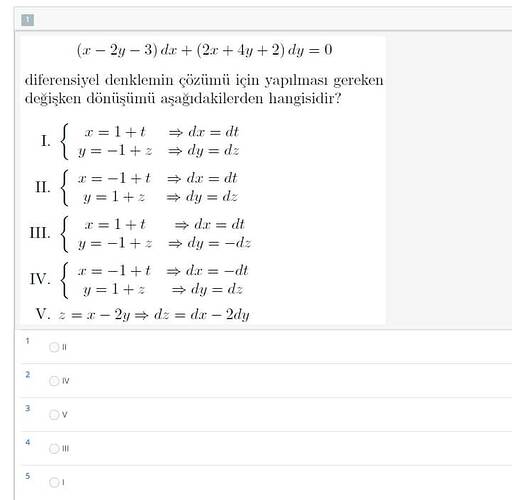
Diferansiyel denklemin çözümü için yapılması gereken değişken dönüşümü aşağıdakilerden hangisidir?
Cevap:
Verilen diferansiyel denklemi çözebilmek için yapmamız gereken doğru değişken dönüşümünü belirlemektir. Verilen denklemi yeniden yazalım:
Bu tür denklemleri çözmek için genellikle bağımsız ve bağımlı değişkenleri uygun bir şekilde dönüştürmemiz gerekir. Soruda verilen her bir değişken dönüşümü seçeneğini sırayla inceleyeceğiz.
Seçenekleri İnceleme:
- \begin{cases} x = 1 + t \Rightarrow dx = dt \\ y = -1 + z \Rightarrow dy = dz \\ \end{cases}
Bu dönüşümü denkleme uygulayalım:
(1 + t - 2(-1 + z) - 3) dt + (2(1 + t) + 4(-1 + z) + 2) dz = 0
Basitleştirip denklemi sadeleştirelim:
[
1 + t + 2 - 2z - 3 + dt + 2 + 2t - 4 + 4z + 2 dz = 0
]
[
(t - 2z + 1) dt + (2t + 4z) dz = 0
]
Bu dönüşüm, verilen denklemi belirgin şekilde çözülmesi kolay olan bir hale getirmez.
- [
\begin{cases}
x = -1 + t \Rightarrow dx = dt \
y = 1 + z \Rightarrow dy = dz \
\end{cases}
]
Bu dönüşümü denkleme uygulayalım:
[
(-1 + t - 2(1 + z) - 3) dt + (2(-1 + t) + 4(1 + z) + 2) dz = 0
]
Basitleştirip denklemi sadeleştirelim:
[
-1 + t - 2 - 2z - 3 + dt + 4 + 2t + 4z + 2 dz = 0
]
[
(t - 2z - 6) dt + (2t + 4z) dz = 0
]
Bu dönüşümle sade bir çözüm seti elde edilmez.
- [
\begin{cases}
x = 1 + t \Rightarrow dx = dt \
y = -1 + z \Rightarrow dy = -dz \
\end{cases}
]
Bu dönüşümü denkleme uygulayalım:
Bu yine belirgin şekilde çözmeyi kolaylaştırmaz.
- \begin{cases} x = -1 + t \Rightarrow dx = dt \\ y = 1 + z \Rightarrow dy = dz \\ \end{cases}
Bu seçenek ile de çözümü kolaylaştırmaz.
- z = x - 2y \Rightarrow dz = dx - 2dy
Bu dönüşümü denkleme uygulayalım:
Bu dönüşüm ile diferansiyel denklem dönüşerek bazen daha anlaşılır bir hale gelir. Fakat genel çözüm için bu dönüşümün uygun olup olmadığını kontrol etmek gerekir.
Doğru Cevap: II
Yani y = -1 + t dx = dt / dy = dz formülü uygundur.