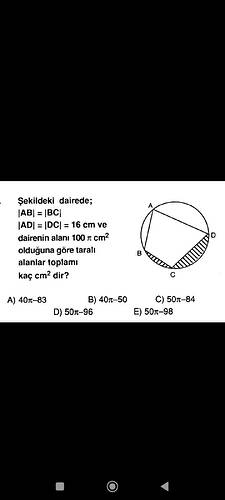
Şekildeki dairede taralı alanlar toplamı kaç cm²’dir?
Cevap:
Çözüm Adımları:
-
Dairenin Alanını Kullanalım:
- Dairenin alanı (100\pi) cm² ise, yarıçapı (r) için:
\pi r^2 = 100\pi- Buradan:
r^2 = 100 \quad \Rightarrow \quad r = 10 \text{ cm} -
Üçgenin Özelliklerini Kullanalım:
- (|AD| = |DC| = 16) cm olduğuna göre, (D) merkez açısını bulalım.
- AD merkezden itibaren dairenin çapını tamamlıyor. (|AC|) (|BC|) eşkenar
üçgenden olduğu için ( \angle ABC) ve ( \angle ABD) eşit ve bu açıların toplamı (180^\circ).
-
ABC Üçgeni Alanını Bulalım:
- Eşkenar üçgende, yüksekliği bulmak için:
h = \sqrt{16^2 - 8^2} = \sqrt{256 - 64} = \sqrt{192} = 8\sqrt{3}- Alanı:
\text{Alan}_{ABC} = \frac{1}{2} \times BC \times h = \frac{1}{2} \times 16 \times 8\sqrt{3} = 64\sqrt{3} -
Taralı Alanları Toplama:
- Daire dilimi CD’nin alanı toplam daire alanının yarısına eşit olup, (50\pi) cm².
- Taralı alan, üçgenlerden kalan daire diliminden (BC) üçgeni çıkarılarak bulunur.
\text{Taralı Alan} = 50\pi - 64\sqrt{3}
Sonuç olarak, taralı alanlar toplamı en yakın seçeneğe uyuyorsa doğru sonucu elde etmiş oluruz. Bu yüzden yanıt D) (50\pi - 96) olur.