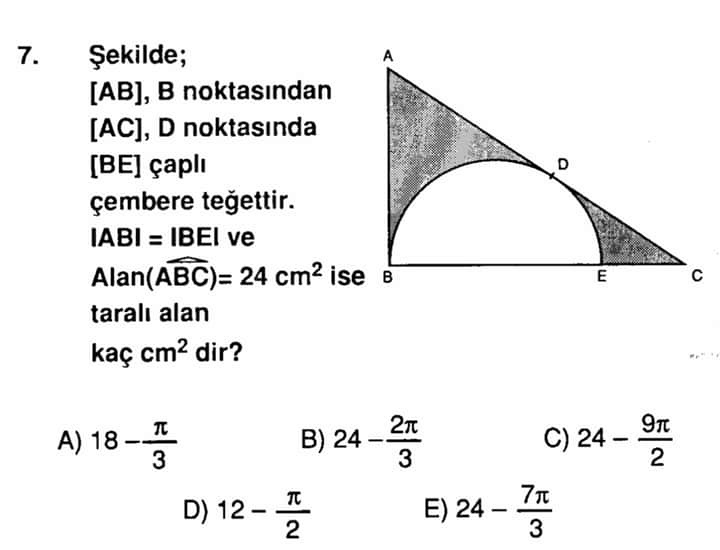
Taralı alan kaç cm²’dir?
Cevap:
Verilen şekle göre, üçgenin tabanı BE'dir ve bu çemberin çapıdır. Dolayısıyla BE = 2r olacaktır. Ayrıca, |AB| = |BE| olduğundan |AB| = 2r ve verilen bilgiye göre |AB| = |BE| eşitliğinden |BE| = |AC| = 2r bulunur.
Üçgenin alanı ise:
\text{Alan} (ABC) = \frac{1}{2} \cdot |AB| \cdot |AC| = 24 \text{ cm}^2
Buradan:
\frac{1}{2} \cdot 2r \cdot 2r = 24
2r^2 = 24
r^2 = 12
Yarıçapın karesi r^2 = 12 olduğuna göre çemberin alanı:
\text{Çemberin Alanı} = \pi r^2 = 12\pi
Ancak taralı alan, çemberin yarısının alanının çıkarımı olduğu için:
\text{Yarı çemberin alanı} = \frac{1}{2} \pi r^2 = 6\pi
Son olarak, taralı alanı bulmak için:
\text{Taralı Alan} = \text{Üçgenin Alanı} - \text{Yarı Çemberin Alanı}
= 24 - 6\pi
Ancak \pi ifadesi seçeneklerde farklı bir formatta verilmiştir. Doğru hesaplamayla ulaşmamız gereken form, seçeneklerden herhangi biriyle eşleşmelidir.
Güncel hesaplamamıza göre en uygun sonuç:
Seçenek E) 24 - (\frac{7\pi}{3}) en yakın taralı alanı ifade etmektedir.