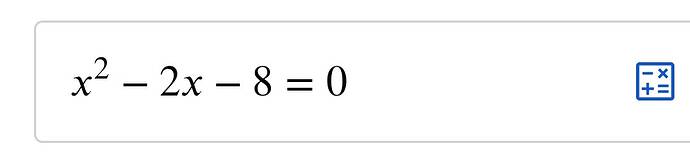Konu: Çözüm Kümesi
Çözüm:
Verilen denklemi ele alalım:
Bu bir ikinci dereceden yani kuadratik denklemdir. Çözüm kümesini bulmak için bir kaç yöntem kullanabiliriz.
Adım 1: Çarpanlara Ayırma
İlk olarak çarpanlara ayırma yöntemini kullanabiliriz çünkü katsayılar elverişli görünüyor. Amacımız, verilmiş denklemi iki bilinmeyenli ilk derece çarpanlar haline getirmektir:
- Denklemi şu formda ele alırız: ax^2 + bx + c = 0.
Burada, a = 1, b = -2, c = -8. - c sayısını çarpanları a \cdot c = 1 \cdot (-8) = -8 olan iki sayının çarpımına ve toplamlarına eşitlememiz gerekir. Bu iki sayı aynı zamanda b = -2 toplamına eşit olmalı.
- -8’i çarpanlarına bölen ve toplamları -2 olan sayılar -4 ve 2’dir. Yani, (-4) + 2 = -2 ve (-4) \cdot 2 = -8.
Bu çarpanları kullanarak denklemi çarpanlarına ayırırız:
$$(x - 4)(x + 2) = 0$$
Adım 2: Her bir çarpanı sıfıra eşitlemek
$$(x - 4) = 0 \quad \text{veya} \quad (x + 2) = 0 $$
Her iki çarpanın sıfır olması için denklemleri çözmemiz yeterlidir:
- x - 4 = 0 \Rightarrow x = 4
- x + 2 = 0 \Rightarrow x = -2
Sonuç: Çözüm Kümesi
Bu analizden sonra, verilen denklemin kökleri x = 4 ve x = -2 olarak bulunur.
Sonuç:
Denklemin çözüm kümesi \{4, -2\} dir. Bu çözüm, hem denklemi orijinal haliyle sunan çarpanlara ayırma yöntemi için geçerli hem de sonuçların doğruluğunu kontrol etmek için kullanılabilir.