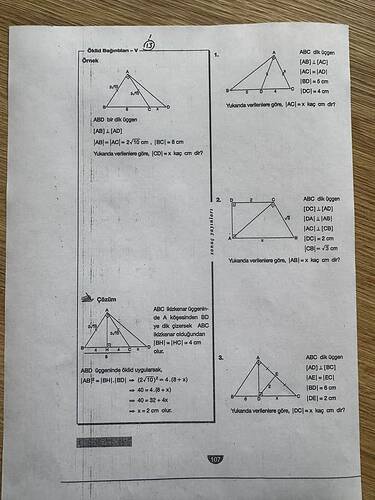
Yukarıdaki Şekilde Verilen Üç ‘Öklid Bağıntıları’ Sorusu Nasıl Çözülür?
Cevap:
Aşağıda, paylaşılan görselde yer alan ve “Öklid Bağıntıları” (dik üçgenlerde yükseklik, kenar ve parçaların çarpımı) ilkelerini gerektiren üç sorunun tipik çözüm yollarını adım adım inceleyeceğiz. Her biri için, dik üçgenin özelliklerinden ve benzeri üçgenlerin (yüksekliğin indirilmesiyle oluşan parçalarda) “Öklid Teoremi” bağıntılarından yararlanılır.
1) Birinci Soru
Şekilde, ABC dik üçgeni verilmiş ve A köşesinden inen dikme BC kenarını B–D–C biçiminde iki parçaya ayırmıştır. Uzunluklar:
- [BD] = 5 cm
- [DC] = 4 cm
- Üçgenin dik açısı: ∠A = 90°
Bu durumda:
-
Hipotenüs uzunluğu:
BC = BD + DC = 5 + 4 = 9 \text{ cm} -
Öklid bağıntıları gereği:
- AB^2 = BD \cdot BC
- AC^2 = DC \cdot BC
- AD^2 = BD \cdot DC (AD, A köşesinden inen dikmenin uzunluğu)
-
Tek tek hesaplayalım:
- AB^2 = 5 \cdot 9 = 45 \implies AB = \sqrt{45} = 3\sqrt{5}
- AC^2 = 4 \cdot 9 = 36 \implies AC = 6
- AD^2 = 5 \cdot 4 = 20 \implies AD = 2\sqrt{5}
Eğer soruda istenen “x” uzunluğu örneğin AB ise x = 3√5 cm, AC ise x = 6 cm, veya “A”dan inen dikmenin uzunluğu (AD) isteniyorsa x = 2√5 cm olur. Ayrıca, A’dan hipotenüsün orta noktasına (G noktası) çizilen “AG” uzunluğu istenirse, dik üçgende hipotenüsün orta noktasına çekilen kenar uzunluğu hipotenüsün yarısıdır; dolayısıyla AG = BC/2 = 4,5 cm.
2) İkinci Soru
Bu kısımda genellikle dörtgen veya bir başka yardımcı çizim kullanılarak dik üçgen ilişkileri tekrar uygulatılır. Soruya göre:
- Dik üçgende, DC ve CB vb. kenar uzunlukları verilir ve [AB] uzunluğu (ya da başka bir kenar) istenir.
- Aynı “Öklid Teoremi” veya Pythagoras ilişkileri üzerinden ilerlenir.
- Gerekirse, üçgen içindeki yükseklik veya benzer üçgenler yardımıyla bilinmeyen kenar (x) bulunur.
Örneğin eğer yine bir dik üçgen söz konusu olup,
- [DC] = 2 cm
- [CB] = 3 cm
- [DB] = 5 cm gibi bir hipotenüs bölme durumu varsa, benzer şekilde
BC = 2 + 3 = 5,
AB^2 = BD \cdot BC vb. formüllerle AB veya AC bulunabilir.
Sorunuzda hangi uzunluğun “x” olarak sorulduğuna göre işlemi aynı adımlarla yapıyoruz: önce hipotenüs veya parçalar toplanır, sonra uygun Öklid bağıntısı ya da Pisagor bağıntısı kullanılarak x değeri hesaplanır.
3) Üçüncü Soru
Burada yine ABC dik üçgeni verilip, ek noktalardan (D, E gibi) inen dikmeler veya eşit parça bilgileri (örneğin [AE] = [EC], [BD] = 6 cm vb.) sunulmuş olabilir. Adım adım yaklaşım:
- İlgili çizimi tam olarak belirleyin. Eşit uzunluklar, ikizkenar durumları veya diklikler (⊥) size benzer üçgenler oluşturur.
- Dik üçgendeki yükseklik (ya da yüksekliklerin ayırdığı parça) uzunlukları arasındaki ilişkiyi Öklid bağıntısıyla kurun:
$$AB^2 = BH \cdot BC, \quad AC^2 = CH \cdot BC,\quad AD^2 = BH \cdot CH \text{ vb.}$$ - Henüz bilinmeyen kenarı (x) bu çarpım veya benzer üçgen teoremleri ile bulun.
Örneğin, eğer [BD] = 6 cm olarak verilip, BC üzerinde başka bir parça [DC] = x isteniyorsa, ve A dik açı ise:
- BC = BD + DC = 6 + x
- Sonra AB^2 veya AC^2 (hangisi verilmişse) yardımıyla bir denklem elde edilir.
- Bu denklemden x çekilerek sonuca varılır.
Özet Tablo
Aşağıda tipik bir dik üçgenin A köşesinden BC üzerine inen dikmesi (D noktası) için gerekli temel bağıntılar özetlenmiştir:
| Bağıntı Adı | Formül | Açıklama |
|---|---|---|
| Hipotenüs Parça Toplamı | BC = BD + DC | B ve C arasındaki toplam uzunluk |
| Birinci Öklid Bağıntısı | AB^2 = BD \cdot BC | A açısı 90° ise, dikkenara karşı kenarın karesi = alt kısımla hipotenüs çarpımı |
| İkinci Öklid Bağıntısı | AC^2 = DC \cdot BC | 90°’nin diğer kenarı için benzer ilişki |
| Üçüncü Öklid Bağıntısı | AD^2 = BD \cdot DC | 90° köşesinden hipotenüse inen dikmenin uzunluğu |
| Dik Üçgende Median | AG = \frac{1}{2}BC | A noktası 90° ise, hipotenüsün orta noktasına çekilen doğru yarım hipotenüstür |
Bu üç sorunun da temeli, dik üçgen ve öklid/pisagor bağıntıları olduğundan, her birinde benzer bir yol izlenir:
- Hipotenüs ve parçaları bulunur.
- Kenarlar arasındaki çarpım/karesel ilişkiler kullanılarak x değeri hesaplanır.
Sonuç ve Kısa Özet
- Dik üçgen içinde yükseklik indirildiğinde hipotenüs iki parçaya bölünür: [BD] ve [DC].
- Kenar uzunlukları, \bigl(AB^2 = BD\cdot BC,\; AC^2 = DC\cdot BC,\; AD^2 = BD\cdot DC\bigr) formülleriyle bulunur.
- Hangi kenar isteniyorsa (x), uygun formülden çekilerek hesaplanır.
- Eğer x, 90°’lik köşeden hipotenüsün orta noktasına çizilen doğru (AG) ise, uzunluk doğrudan hipotenüsün yarısına eşittir.
Bu adımları uygulayarak, paylaşılan görseldeki üç farklı soru da benzer şekilde çözümlenir.