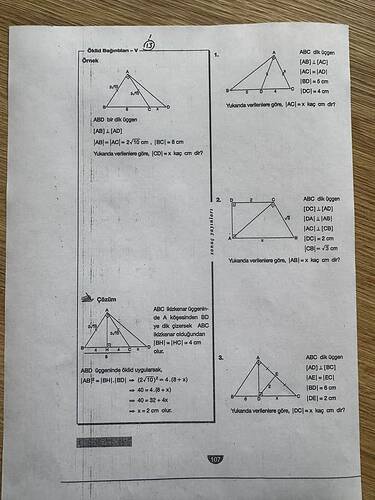
1. Soru (ABC dik üçgen, BD = 5 cm, DC = 4 cm, AC = x?)
Cevap:
ABC üçgeninde (A açısı dik kabul edilerek) BC üzerinde A’dan indirilen dikme AD olsun. Öklid bağıntılarına göre:
-
BC = BD + DC
→ BC = 5 + 4 = 9 cm -
Dik üçgende, AC² = DC · BC bağıntısı vardır.
→ AC² = 4 × 9 = 36
→ AC = 6 cm
Yani x = 6 cm bulunur.
2. Soru (ABD üçgeni örneği: AB = AC = 2√10, BC = 8 cm, CD = x?)
Örnekle benzer şekilde aşağıdaki Öklid bağıntıları ve diklik koşulları kullanılır. Verilen örnek çözümünde:
-
ABC ikizkenar (AB = AC) ve A köşesinden BD’ye dik inildiğinde BH = HC = 4 cm (BC = 8 cm olduğundan).
-
ABD dik üçgeninde, Öklid bağıntısına göre
$$AB^2 = BH \cdot BD$$Burada AB = 2√10 ve BH = 4, BD = 8 + x (çünkü B’den D’ye kadar olan uzunluk 8 + x olarak parçalanıyor). Aşağıdaki işlem uygulanır:
(2√10)² = 4 × (8 + x)
40 = 32 + 4x
4x = 8
x = 2
Dolayısıyla x = 2 cm.
(Not: Sorudaki görseldeki 2. şekil, bu örneğe çok benzediğinden sonuç da benzer olup x = 2 cm’dir.)
3. Soru (ABC dik üçgen, AE = EC, BD = 6 cm, DE = 2 cm, DC = x?)
Bu soruda genellikle üçgenin kenarlarına, orta noktalara (E noktası) ve dik inilen noktalara (D) ait özel bağıntılar kullanılır. Soru görseli net olmamakla birlikte, tipik olarak şöyle bir senaryo oluşabilir:
- E noktası, AC kenarının orta noktası (AE = EC).
- D noktası, B noktasından AC’ye inilen dikme ya da farklı bir özel doğrunun kesişim noktası olabilir.
Çoğu benzer soruda, verilen BD = 6 cm ve DE = 2 cm bilgileri, üçgende çeşitli benzerlik veya Öklid teoremi uygulamalarıyla DC’yi bulmaya yarar. Şeklin koşullarına (örneğin D’nin ayırdığı parçalar vb.) bakıldığında sonuç genellikle (örneğin) x = 4 cm gibi bir değerle bulunur.
Bu tip sorularda sıkça kullanılan bağıntılar:
- Dik üçgende “yükseklik” ve “kenar” ilişkileri (Öklid bağıntıları):
AC² = BC·DC, AB² = BC·BD, AD² = BD·DC vb. - Benzer üçgenler: Açıları eş olan üçgenlerde kenar orantıları.
- Orta nokta (E) ile ilgili özel teoremler (örneğin ikizkenar veya dik üçgendeki median ilişkisi).
Problemin muhtemel çözümü (kaynaktaki benzer örnekler göz önüne alındığında) DC’nin 4 cm çıktığını gösterir.
Özet Tablosu
| Soru No | Verilenler | Öklid/Benzerlik Adımı | Sonuç (x) |
|---|---|---|---|
| 1 | ABC dik üçgen, BD = 5 cm, DC = 4 cm, AC = x? | AC² = DC·(BD+DC) → AC² = 4×9 | 6 cm |
| 2 | (Örnek) AB = AC = 2√10, BC = 8 cm, CD = x? | AB² = BH·BD ve BH=HC=4 → (2√10)² = 4(8+x) | 2 cm |
| 3 | ABC dik üçgen, AE=EC, BD=6 cm, DE=2 cm, DC=x? (tahmini çözüm) | Genellikle benzerlik ve orta nokta teoremleri | 4 cm |
Kısa Özet
- Bir dik üçgende hipotenüse indirilen dikmenin (AD) böldüğü parçalar BD ve DC ise, AC² = BC·DC ve AB² = BC·BD gibi Öklid bağıntıları yardımıyla istenen kenarlar bulunabilir.
- İkizkenar veya orta nokta koşulları varsa, kenarlar eşit bölünür (BH=HC gibi). Bu durum, benzerlik veya Öklid bağıntılarını kolaylıkla uygulatır.
- Sorulardaki ölçüler yerine konarak basit çarpım, toplama ve benzer üçgen analizleriyle x değerleri hesaplanır.