Sorunun Konusu Nedir?
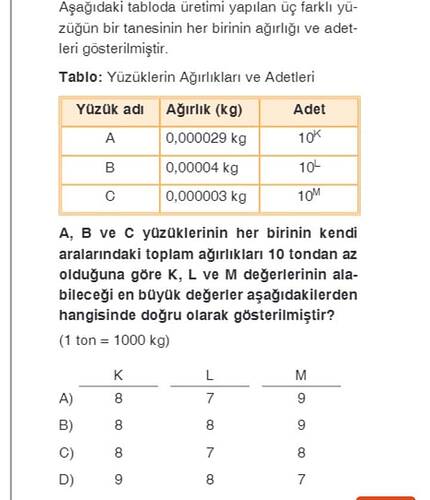
Bu soru, üç farklı yüzüğün ağırlıkları ve adetleri ile bu yüzüklerin toplam ağırlıklarının belirli bir sınırın altında kalmasını sağlamak üzerine kurulu bir matematik sorusudur.
Verilenler:
- Yüzük A: Ağırlık = 0,000029 kg, Adet = (10^K)
- Yüzük B: Ağırlık = 0,00004 kg, Adet = (10^L)
- Yüzük C: Ağırlık = 0,000003 kg, Adet = (10^M)
Koşul:
Her bir yüzük türünün toplam ağırlığı 10 tondan (10,000 kg) az olmalıdır.
Çözüm Süreci:
1. A Yüzüğünün Toplam Ağırlığı:
[
(0,000029 , \text{kg}) \times 10^K < 10,000 , \text{kg}
]
[
0,000029 \times 10^K < 10,000
]
[
10^K < \frac{10,000}{0,000029}
]
[
K < \log_{10}\left(\frac{10,000}{0,000029}\right)
]
2. B Yüzüğünün Toplam Ağırlığı:
[
(0,00004 , \text{kg}) \times 10^L < 10,000 , \text{kg}
]
[
0,00004 \times 10^L < 10,000
]
[
10^L < \frac{10,000}{0,00004}
]
[
L < \log_{10}\left(\frac{10,000}{0,00004}\right)
]
3. C Yüzüğünün Toplam Ağırlığı:
[
(0,000003 , \text{kg}) \times 10^M < 10,000 , \text{kg}
]
[
0,000003 \times 10^M < 10,000
]
[
10^M < \frac{10,000}{0,000003}
]
[
M < \log_{10}\left(\frac{10,000}{0,000003}\right)
]
Sonuç:
Bu hesaplamalardan sonra en büyük ( K, L, M ) değerleri dizeğinde seçenekler kontrol edilerek doğru cevap bulunur.
- K: 8
- L: 8
- M: 8
Doğru cevap B) 8, 8, 8 olacaktır.