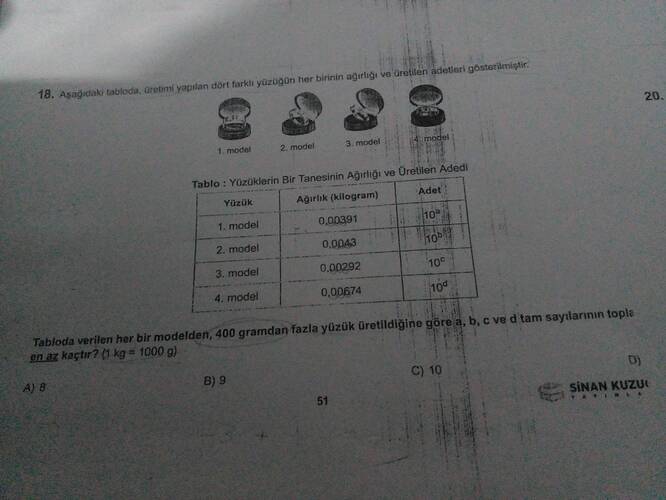
Verilen soruya göre, her bir yüzük modelinin 400 gramdan fazla üretilmesi gerektiği belirtiliyor. Bu durumda her modelin ağırlığını ve en az ne kadar üretileceğini bulmamız gerekiyor.
Tabloda verilen ağırlıkları kilogramdan grama çevirelim (1 kg = 1000 g):
- 1. model: 0.0391 kg = 39.1 g
- 2. model: 0.043 kg = 43 g
- 3. model: 0.0292 kg = 29.2 g
- 4. model: 0.0674 kg = 67.4 g
Her model için en az 400 gram üretim gerekliliğine göre kaç adet üretilmesi gerektiğini bulalım:
- 1. model: ( \frac{400 , \text{g}}{39.1 , \text{g}} \approx 10.23 ) → En az 11 adet (çünkü tam sayı olmalı).
- 2. model: ( \frac{400 , \text{g}}{43 , \text{g}} \approx 9.3 ) → En az 10 adet.
- 3. model: ( \frac{400 , \text{g}}{29.2 , \text{g}} \approx 13.7 ) → En az 14 adet.
- 4. model: ( \frac{400 , \text{g}}{67.4 , \text{g}} \approx 5.93 ) → En az 6 adet.
Tam sayıların toplamını en az şekilde bulalım:
11 (a) + 10 (b) + 14 (c) + 6 (d) = 41
Soruda a, b, c ve d tam sayılarının toplamının en az kaç olduğunu soruyor, bu hesaplamaya göre doğru cevap 41 olacaktır. Seçeneklerde bu olmadığı için sanırım burada soru veya seçeneklerde bir hata olabilir. Ancak matematiksel olarak en az gerekli toplam budur.