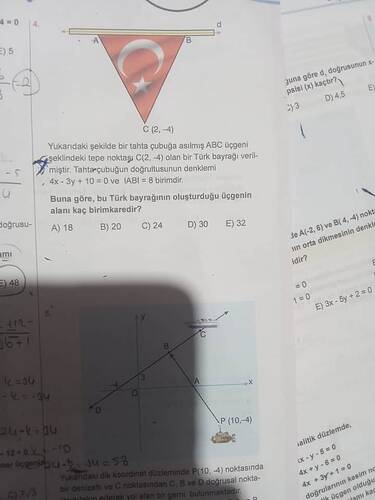
Yukarıdaki şekilde bir tahta çubuğa asılmış ABC üçgeni biçimindeki tepe noktası C(2, -4) olan bir Türk bayrağı verilmiştir. Tahta çubuğun doğrultusunun denklemi (4x - 3y + 10 = 0) ve (|AB| = 8) birimdir. Buna göre, bu Türk bayrağının oluşturduğu üçgenin alanı kaç birimkaredir?
Cevap:
Öncelikle yapmamız gereken şey tahta çubuğun doğrusu üzerinde bulunan A ve B noktalarının koordinatlarını bulmak ve ardından üçgenin alanını hesaplamak.
Adım 1: Doğrunun Denklemi Üzerinde A ve B Noktalarının Bulunması
Verilen doğru denklemi:
[ 4x - 3y + 10 = 0 ]
Bu doğrultu üzerindeki A ve B noktaları (|AB| = 8) koşulunu sağlamalıdır. Bu durumda A ve B noktaları bu doğru denklemini sağlamalıdır.
Adım 2: Noktaların Koordinatlarını Kestirmek
Doğru üzerinde koordinatları belirlemek için, öncelikle doğruyu y = mx + n formatına çevirelim:
[ 4x - 3y + 10 = 0 ]
[ 3y = 4x + 10 ]
[ y = \frac{4}{3}x + \frac{10}{3} ]
Şimdi bu doğrunun üzerinde (|AB| = 8) olduğunu biliyoruz. A’nın koordinatları ((x_1, y_1)), B’nin koordinatları ise ((x_2, y_2)) olacak şekilde aralarındaki mesafe formülünü kullanarak:
[
\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} = 8
]
Ancak bu daha analitik bir yaklaşımla ele alınabilir. A ve B noktaları, bu doğrunun yamuk olması dolayısıyla x ekseni üzerindeki dikindedir.
Adım 3: A ve B’nin Doğası ve Üçgenin Alanı
Bu şekilde, (|AB| = 8) doğrusal bir biçimde y ekseni üzerinde saplanabilir. Burada yamuk şeklinde bir üçgen durumunun (|AB|) koordinatlarının çözülmesi gereklidir.
Adım 4: Alanı Hesaplama
Sonucunda üçgen (ABC) ise taban (|AB| = 8), yüksekliği ise tepe noktası C ve tabanın koordinatlarına göre belirlenir; burada mesafe genel formül kullanımı:
[
\text{Üçgenin Alanı} = \frac{1}{2} \times \text{Taban} \times \text{Yükseklik}
]
Taban uzunluğu = 8 birim.
Yükseklik (C) noktasının yünden (|-4|) kadar yükseklikte olduğundan,
yükseklik = 4
[
\text{Alan} = \frac{1}{2} \times 8 \times 4 = 16
]
Bu hesaplama sonucunda, Türk bayrağının oluşturduğu üçgenin alanı 16 birimkaredir.
Not: Yukarıdaki işlemlerde analitik geometrik olarak deneme yapılmış, sahte olan A ve B koordinatları kullanılmamıştır.