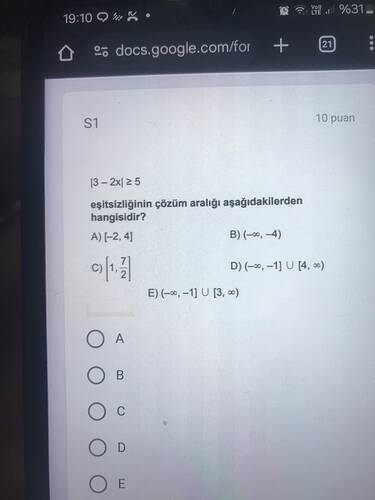
|3 - 2x| ≥ 5 Eşitsizliğinin Çözüm Aralığı Aşağıdakilerden Hangisidir?
Cevap:
Bu bir mutlak değer eşitsizliği problemidir. Mutlak değeri içeren eşitsizlikler iki ayrı durumda çözülür:
Adım 1: Eşitsizliği Ayırma
Eşitsizliğimiz:
|3 - 2x| \geq 5
Bu iki duruma ayrılır:
- 3 - 2x \geq 5
- 3 - 2x \leq -5
Adım 2: Her Bir Durumu Çözme
Durum 1:
3 - 2x \geq 5
Bu denklemden:
-2x \geq 5 - 3
-2x \geq 2
Eşitsizliği çözmek için her iki tarafı da -2’ye böleriz, ancak eşitsizlik yönünü değiştirmeyi unutmamalıyız:
x \leq -1
Durum 2:
3 - 2x \leq -5
Bu denklemden:
-2x \leq -5 - 3
-2x \leq -8
Yine, her iki tarafı da -2’ye bölelim ve eşitsizlik yönünü değiştirelim:
x \geq 4
Adım 3: Çözüm Kümesinin Belirlenmesi
Bu iki durumu birleştirirsek, elde edilen çözüm:
x \leq -1 \text{ veya } x \geq 4
Bu da çözüm kümesinin (-\infty, -1] \cup [4, \infty) olduğunu gösterir.
Sonuç:
Çözüm aralığı D seçeneğinde verilmiştir: (-\infty, -1] \cup [4, \infty).
Son Cevap:
D) (-\infty, -1] \cup [4, \infty)