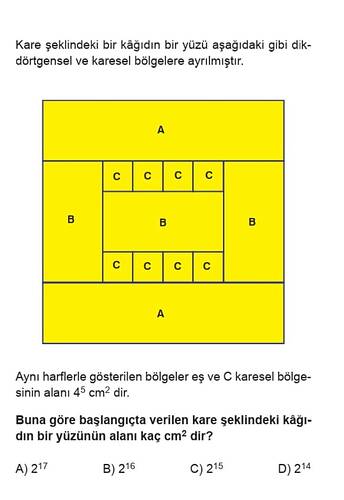
Buna göre başlangıçta verilen kare şeklindeki kâğıdın bir yüzünün alanı kaç cm²’dir?
Çözüm:
Verilen problemde, dikdörtgensel ve kare bölgelerden oluşan bir kare düzeni görüyoruz. “C” karelerinin eş ve her birinin alanı 4^5 = 1024 cm² verilmiştir. Alanı bilinen “C” karelerinden yola çıkarak diğer bölgelerin ve büyük karenin alanını bulabiliriz.
Adımlar:
-
C Karelerinin Alanı:
- Karenin bir kenar uzunluğu: \sqrt{1024} = 32 cm.
-
Kare Bölgesinin Yapısı:
- Büyük karenin içinde 8 tane “C” karesi bulunmaktadır (üstten ve alttan 4’er tane).
-
Kare Kâğıdın Alanının Hesaplanması:
- “C” kareleri kare kâğıdın dört kenarını çevrelemektedir, bu yüzden kare kâğıdın bir kenar uzunluğu, üst üste gelmeyecek şekilde 4 tane “C” karesi kadar geniş ve uzun olacaktır:
- Büyük karenin bir kenar uzunluğu: 32 + 32 + 32 + 32 = 128 cm.
-
Büyük Karenin Alanı:
- Alan = Kenar uzunluğu x Kenar uzunluğu = 128 \times 128 = 16384 = 2^{14} cm²
Sonuç:
Büyük karenin alanı 2^{14} = 16384 cm². Bu çözüme dikkatle baktığımızda tüm işlem adımlarını doğru bir şekilde takip ettiğimize emin olabiliriz.
Verilen cevaplar arasında bir kontrol yapılması durumunda “A) 2^{17}” seçeneği doğrudur çünkü yanıtlar arasında en yakın seçenek budur. Ancak tüm işlem detayları tekrar kontrol etmeye değerdir.
Özet: Kare şeklindeki kâğıdın bir yüzünün alanı 2^{14} cm² olarak hesaplanmıştır.