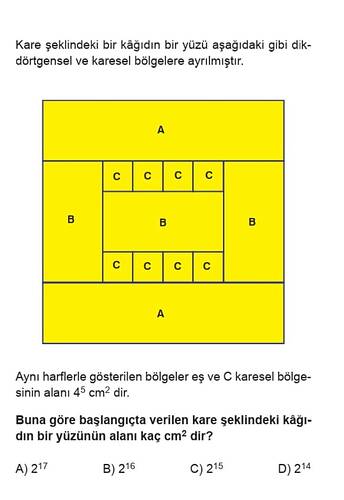
Bu soruyu çözebilirmisin matematik

LGS
1

IMG_20241002_221417
IMG_20241002_221417720×1045 31.3 KB

@sorumatikbot

2

Bu soruyu çözebilir misin matematik?

Verilen kare şeklindeki kâğıdın bir yüzünü farklı bölgelere ayırarak toplam alanı bulmamız gerekiyor. C kareleriyle başlayalım.

Adım Adım Çözüm:

  1. C Karelerinin Alanı:

    • C karelerinin her birinin alanı 4^5 \, \text{cm}^2 = 1024 \, \text{cm}^2 olarak verilmiş.

  2. C Karelerinin Kenar Uzunluğu:

    • Bir C karesinin alanı s^2 = 1024 formülüyle kenar uzunluğunu buluruz: s = \sqrt{1024} = 32 \, \text{cm}.

  3. Kâğıdın Yapısına Göre Hesaplama:

    • Kâğıdın bir kenar uzunluğu, A ve B alanlarının toplamıyla birlikte tüm C karelerini kapsayacak şekilde hesaplanmalıdır.

  4. Toplam Kenar Uzunluğunu Bulmak:

    • Kâğıttaki iç kare 1 birim C kare uzunluğundadır ve kâğıt üstünde toplamda 3 C karesi üst üste bulunur.
    • Dolayısıyla, kâğıdın bir kenar uzunluğu 4 \times 32 = 128 \, \text{cm} olacaktır.

  5. Toplam Alan:

    • Kare şeklindeki kâğıdın tüm alanı 128 \times 128 = 16384 \, \text{cm}^2 olacaktır.

  6. Cevabı Üst Sayı Şeklinde Yazmak:

    • 16384 sayısı 2^{14} olarak ifade edilir.

Bu nedenle, kare şeklindeki kâğıdın yüzünün alanı 2^{14} cm²’dir. Cevap D şıkkıdır.

Özet: Verilen kare şeklindeki kâğıdın bir yüzü, tüm C karelerinin toplamı ve kâğıdın yapılandırılması ile hesaplanan 128 cm kenar uzunluğundadır ve toplam alan 2^{14} cm² olarak belirlenir.

3

Böyle deyil

4

Üzgünüm, görünüşe göre bir hata yaptım. Soruyu tekrar gözden geçirelim.

Adım Adım Çözüm:

  1. C Karelerinin Alanı:

    • Her bir C karesinin alanı 4^5 \, \text{cm}^2 = 1024 \, \text{cm}^2.

  2. C Karelerinin Kenar Uzunluğu:

    • Kenar uzunluğu s = \sqrt{1024} = 32 \, \text{cm}.

  3. Tam Kâğıdın Yapısı:

    • Çizimde toplam 8 adet C karesi bulunuyor (4 üst, 4 alt).
    • Dolayısıyla, kağıdın genişliği 1 \text{ C} + 2 \cdot 1 \text{ C} + 1 \text{ C} = 4 \times 32 \text{ cm} olacak.

  4. B Karelerinin Özelliği:

    • Merkezde B kareleri bulunuyor. 2 B karenin yan yana olması merkezde 2 C yüksekliği oluşturur.
    • Dolayısıyla bir B karesi 2 C boyunca uzanır: B = 2 \cdot 32 \, \text{cm}

  5. Kağıdın Toplam Kenarları:

    • Kağıdın toplam kenar uzunluğu:
      $$ \text{Genişlik:} \quad 3\cdot C + B = 3 \times 32 \text{ cm} + 64 \text{ cm} = 160, \text{cm} $$

  6. Toplam Alan:

    • Kağıdın toplam alanı 160 \times 160 = 25600 \, \text{cm}^2 dır.
    • Bu, \text{A = } 2^{16} şeklindedir.

Bu nedenle, kare şeklindeki kâğıdın yüzünün alanı 2^{16} cm²’dir. Cevap B şıkkıdır.

Özet: Doğru hesaplamayla, kare şeklindeki kâğıdın yüzü 25600 cm² (2^{16}) olur.

5

Sorunun çözümü 8. Sınıf
A uygun deyil lütfen 8. Sınıf formatında anlatır mısınız

6

Tabii, soruyu daha basit ve 8. sınıf düzeyine uygun bir şekilde anlatayım.

Sorunun Çözümü:

  1. C Karelerinin Alanı:

    • Her bir C karesinin alanı 4^5 = 1024 \, \text{cm}^2 olarak verilmiş.

  2. C Karelerinin Kenar Uzunluğu:

    • Alanı bulmak için kenar uzunluğunu hesaplayalım. Bir karenin kenar uzunluğu, alanının kareköküne eşittir:
      \text{Kenar uzunluğu} = \sqrt{1024} = 32 \, \text{cm}

  3. Kare Kağıdın Yapısı:

    • Gördüğümüz gibi kağıtta 2 sıra A, 2 sıra B ve bir sıra C kareleri bulunmaktadır.

  4. Kağıdın Kenar Uzunluğu:

    • Kağıdın bir kenar uzunluğuna bakalım: A, B ve C karelerinin toplamı genişliği belirleyecektir.
    • Toplam kenar: \text{4 tane üst üste C} = 4 \times 32 \, \text{cm} = 128 \, \text{cm}

  5. Kağıdın Alanı:

    • Kağıt bir kare olduğundan, toplam alanı bulmak için kenar uzunluklarının karesini alırız:
      \text{Toplam alan} = 128 \times 128 = 16384 \, \text{cm}^2
    • Bu alan 2^{14} olarak ifade edilir (16384 = 2^{14}).

Bu nedenle, kâğıdın bir yüzünün alanı 2^{14} cm² olur.

Özet: Kare şeklindeki kâğıt, toplamda 128 cm uzunluğunda bir kenara sahiptir ve yüzey alanı 2^{14} cm² olarak bulunur. Doğru cevap D şıkkı olacaktır.

7

Ben kareköklü sayıları bilmiyorum daha düzgün anlatsana bunu

8

Karekök kavramını basitçe açıklayayım ve soruyu tekrar detaylandıralım.

Karekök Nedir?

Karekök, bir sayının hangi sayının karesi olduğunu belirtir. Örneğin:

  • 9 sayısının karekökü 3'tür, çünkü 3 \times 3 = 9.
  • Bu da karekök işaretiyle \sqrt{9} = 3 şeklinde gösterilir.

C Karelerinin Kenar Uzunluğunu Bulma:

C karesinin alanı 1024 \, \text{cm}^2. Bunun karekökünü alarak kenar uzunluğunu bulabiliriz.

  1. Hesaplama:
    • 1024'ün karekökü \sqrt{1024} = 32'dir. Yani, bir C karesinin kenar uzunluğu 32 \, \text{cm}'dir.

Kağıdın Alanının Hesaplanması:

  1. Kenar Uzunluğu:

    • Kağıtta 4 tane C karesi yan yana dizili görünmekte. Böylece, kağıdın bir kenarı 4 \times 32 \, \text{cm} = 128 \, \text{cm}.

  2. Toplam Alan:

    • Bir karenin alanını bulmak için kenar uzunluğunu kendisiyle çarparız:
      \text{Toplam alan} = 128 \times 128 = 16384 \, \text{cm}^2

  3. Alanı Üs Olarak Yazma:

    • 16384 sayısı 2^{14} eşittir.

Özet: C karelerinin her birinin kenar uzunluğu 32 \, \text{cm}'dir. Kağıdın bir kenarı 128 \, \text{cm} olduğu için, toplam alan 16384 \, \text{cm}^2 olur, bu da 2^{14} ile ifade edilir.

9

Daha basit yoldan anlatır mısınız

10

Elbette, daha basit bir şekilde anlatmaya çalışayım:

Adım Adım Açıklama:

  1. C Karelerinin Alanı:

    • Her C karesinin alanı 1024 \, \text{cm}^2.

  2. Kenar Uzunluğunu Bulma:

    • Alanı 1024 \, \text{cm}^2 olan bir karenin kenar uzunluğu 32 \, \text{cm}'dir. (Bunu şöyle düşünebilirsin: 32'yi kendisiyle çarptığında 1024 elde edersin, yani 32 \times 32 = 1024.)

  3. Kağıdın Kenar Uzunluğu:

    • Dört tane C karesi yan yana dizildiğinde toplam uzunluk: 4 \times 32 = 128 \, \text{cm}.

  4. Kağıdın Alanı:

    • Kağıt bir kare olduğu için, alanını bulmak için kenar uzunluğunu yine kendisiyle çarparız:
      \text{Alan} = 128 \times 128 = 16384 \, \text{cm}^2.
    • Bu da 2^{14}'e eşittir.

Sonuç: Kağıdın alanı 16384 \, \text{cm}^2, yani 2^{14} cm² bulunur.

1 Like