Böyle soruları yapamıyorum ya sinir oluyom

YKS TYT
1

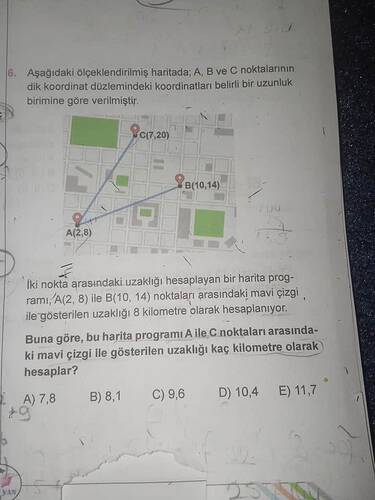
17379213786494627202052497687803
17379213786494627202052497687803720×960 41.3 KB

2

Aşağıdaki ölçeklendirilmiş haritada; A, B ve C noktalarının dik koordinat düzlemindeki koordinatları belirli bir uzunluk birimine göre verilmiştir.

Verilen koordinatlar:

  • ( A(2, 8) )
  • ( B(10, 14) )
  • ( C(7, 20) )

İki nokta arasındaki uzaklığı hesaplayan bir harita programı, ( A(2, 8) ) ile ( B(10, 14) ) noktaları arasındaki mavi çizgi ile gösterilen uzaklığı 8 kilometre olarak hesaplanıyor.

Programın hesapladığı mesafe, iki nokta arasındaki Öklidyen mesafe üzerinde ölçeklendirilmiş. Yani doğrusal mesafeyi bir ölçü birimine çeviriyorlar. Öncelikle bu ölçek faktörünü bulmamız gerekiyor.

A ile B arasındaki Öklidyen mesafeyi hesaplayalım:

Uzunluk formülü:

d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}

A ve B arasındaki mesafe:

d_{AB} = \sqrt{(10 - 2)^2 + (14 - 8)^2} = \sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10

Bu durumda, bu 10 birimlik mesafe 8 kilometreye karşılık geliyor. Ölçek faktörü:

k = \frac{8}{10} = 0.8

Buna göre, A ile C noktaları arasında mavi çizgi ile gösterilen uzaklığı hesaplayalım.

A ile C arasındaki mesafe:

d_{AC} = \sqrt{(7 - 2)^2 + (20 - 8)^2} = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13

Bu mesafeyi ölçek faktörüne göre kilmetreye çevirelim:

d_{AC}' = 13 \times 0.8 = 10.4

Bu nedenle, bu harita programı, A ile C noktaları arasındaki mavi çizgi ile gösterilen uzaklığı 10.4 kilometre olarak hesaplar. Doğru cevap D şıkkıdır: 10.4.