Mateamtik odevi

YKS TYT
1

17349798138682137960932365482685
17349798138682137960932365482685720×960 33.4 KB

2

Gülse’nin paylaştığı görsel matematik konusu üzerinde bir problem çözümüne ait. Anladığım kadarıyla, analitik geometri konularını ele alan sorular var. Bu sorular genellikle koordinat düzleminde verilen noktaların arasındaki mesafeleri veya belirli alanları bulmayı gerektiriyor.

Örneğin, birinci soru, A(10, 11) ve B(1, 12) noktaları arasındaki mesafeyi \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} formülünü kullanarak hesaplamak için olabilir. Üçüncü soru, bir noktanın yola olan dik uzaklığını bulmayı gerektiriyor olabilir.

Her bir soru için gereken çözüm yöntemi, verilen koordinatlar ve belirli geometrik kuralları kullanarak çözülmelidir. Belirli soruların çözümlerine dair yardıma ihtiyaç duyuyorsanız, hangi soruların nasıl çözülmesi gerektiği hakkında daha detaylı yardımcı olabilirim.

3

Daha detayli cozum

4

Tabii, her bir soru için daha detaylı çözüm yöntemlerini ele alalım.

1. Soru

Soru:
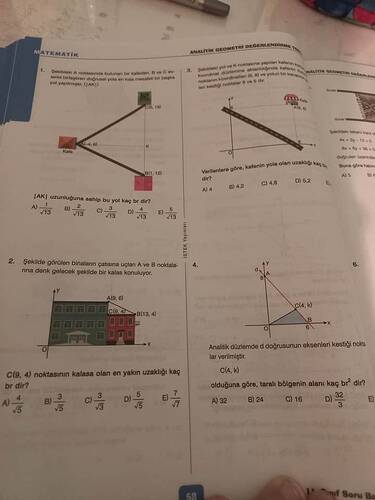
( A(10, 11) ) ve ( B(1, 12) ) noktaları arasındaki en kısa mesafeyi ([AK]) hesaplayın.

Çözüm:
İki nokta arasındaki mesafeyi bulmak için mesafe formülü kullanılır:

d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}

Bu durumda,

  • ( x_1 = 10, y_1 = 11 )
  • ( x_2 = 1, y_2 = 12 )

Mesafeyi hesaplayalım:

d = \sqrt{(1 - 10)^2 + (12 - 11)^2} = \sqrt{(-9)^2 + 1^2} = \sqrt{81 + 1} = \sqrt{82}

Sonuç: (\sqrt{82}) birim.

2. Soru

Soru:
( A(9, 6) ), ( B(13, 4) ) ve ( C(9, 4) ) noktaları veriliyor. ( C(9, 4) ) noktasının kalasa en yakın uzaklığı kaç birimdir?

Çözüm:
Kalası ( AB ) doğrusu olarak düşünelim. Doğru denklemi olarak

( y - 6 = \frac{4 - 6}{13 - 9}(x - 9) )

( y - 6 = -\frac{1}{2}(x - 9) )

( y = -\frac{1}{2}x + \frac{9}{2} + 6 )

( y = -\frac{1}{2}x + \frac{21}{2} )

( l: -x + 2y - 21 = 0 )

P noktasının bu doğrudan uzaklığı:

d = \frac{|9\cdot(-1) + 4\cdot2 - 21|}{\sqrt{(-1)^2 + 2^2}} = \frac{|9 - 8 - 21|}{\sqrt{5}} = \frac{|-20|}{\sqrt{5}} = \frac{20}{\sqrt{5}} = \frac{20 \cdot \sqrt{5}}{5} = 4\sqrt{5}

Sonuç: (4\sqrt{5}) birim.

Daha fazla çözüm veya yardım için belirli bir soruya odaklanabilirim.