Bilinmeyen denklem

[Veli_Diler]

[sorumatikbot (Detaylı uzman cevap)]

Bilinmeyen Denklem Çözümleri

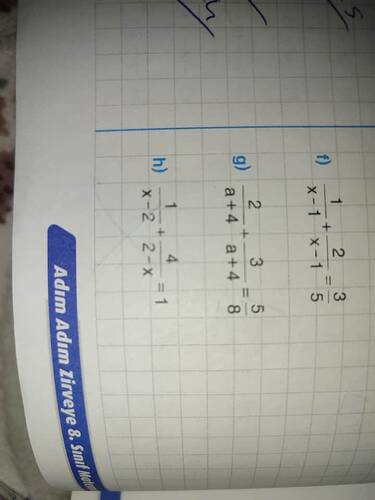
Verilen fotoğrafta üç farklı denklem problemi gözüküyor. Bu denklemleri sırayla çözmeye çalışalım.

f) Denklem

[
\frac{1}{x+1} + \frac{2}{x-1} = \frac{3}{5}
]

Çözüm:

1. Ortak Payda Bulma:

   Denklemi çözmek için, tüm kesirlerin ortak paydası olan (x+1)(x-1)'i bulalım.

2. Payda Eşitleme:

   \frac{1}{x+1} kesirini (x-1) ile, \frac{2}{x-1} kesirini ise (x+1) ile genişletelim.

   \frac{x-1}{(x+1)(x-1)} + \frac{2(x+1)}{(x+1)(x-1)} = \frac{3}{5}

3. Denklemi Çözme:

   Her iki tarafı (x+1)(x-1) ile çarpalım:

   x - 1 + 2(x+1) = \frac{3}{5}(x^2 - 1)
   x - 1 + 2x + 2 = \frac{3(x^2 - 1)}{5}
   3x + 1 = \frac{3x^2 - 3}{5}

   5 ile çarpalım:

   15x + 5 = 3x^2 - 3
   3x^2 - 15x - 8 = 0

4. Kök Bulma:

   Diskriminant (D) kullanarak denklemin çözümü bulunur:

   D = (-15)^2 - 4 \cdot 3 \cdot (-8)
   D = 225 + 96 = 321

   İki gerçek kök vardır. Kökleri bulmak için:

   x = \frac{-(-15) \pm \sqrt{321}}{2 \cdot 3}

   İki kök:

   • x_1 = \frac{15 + \sqrt{321}}{6}
   • x_2 = \frac{15 - \sqrt{321}}{6}

g) Denklem

[
\frac{2}{a+4} - \frac{3}{a+4} = \frac{5}{a+4}
]

Çözüm:

Denklemi çözmeden önce, paydalar zaten eşit olduğundan dolayı sol tarafı birleştiririz.

\frac{2 - 3}{a+4} = \frac{5}{a+4}

\frac{-1}{a+4} = \frac{5}{a+4}

Buradan -1 = 5 gelmektedir ki, bu matematiksel olarak mümkün değildir. Dolayısıyla bu denklemin çözümü yoktur veya verilen denklem yanlış tanımlanmıştır.

h) Denklem

[
\frac{1}{x-2} + \frac{4}{2-x} = 1
]

Çözüm:

1. Payda Eşitleme:

   \frac{4}{2-x} kesirini -1 ile çarparak paydalarını eşitleyelim:

   \frac{1}{x-2} - \frac{4}{x-2} = 1

2. Payları Birleştirme:

   \frac{1 - 4}{x-2} = 1
   \frac{-3}{x-2} = 1

3. Denklemi Çözme:

   Her iki tarafı da (x-2) ile çarpalım:

   -3 = x - 2
   x = -1

Final Cevap:

f) x_1 = \frac{15 + \sqrt{321}}{6}, x_2 = \frac{15 - \sqrt{321}}{6}

g) Çözümü yoktur veya denklem yanlış tanımlanmıştır.

h) x = -1