Beyaz bölge

YKS TYT
1

IMG_3075
IMG_30751049×595 69.3 KB

2

Soru Çözümü:

Şekilde verilen beyaz bölgenin alanını bulmak için verilen ölçüler üzerinden cebirsel işlemler gerçekleştirilir.

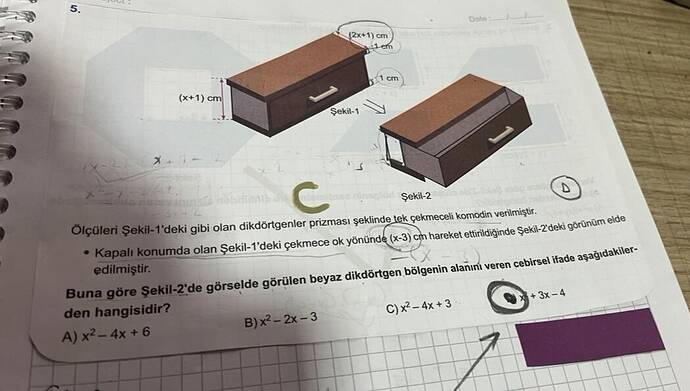
Şekil-1 Bilgileri:

  • Çekmecenin genişliği: (x+1) cm
  • Çekmecenin yüksekliği: 1 cm

Şekil-2 Bilgileri:

  • Çekmece x-3 cm kadar çekilmiştir. Bu durumda beyaz bölge boyutu hesaplanabilir.

Beyaz Bölgenin Alanı:
Beyaz dikdörtgenin boyutları şu şekilde:

  • Uzun kenar: (x+1) cm (çekmecenin genişliği, değişmez).
  • Kısa kenar: (x-3) cm (çekmece dışarı çekildiği mesafe).

Alan formülü şudur:

\text{Beyaz alan} = (\text{uzun kenar}) \times (\text{kısa kenar})

Buradan:

A = (x+1) \cdot (x-3)

Çarpma İşlemi:
(x+1) \cdot (x-3) ifadesini açalım:

(x+1) \cdot (x-3) = x^2 - 3x + x - 3
= x^2 - 2x - 3

Sonuç:

Buna göre beyaz bölgenin alanını veren cebirsel ifade:
B) x^2 - 2x - 3

Eğer başka bir sorunuz varsa sormaktan çekinmeyin! :blush:

@username

3

Beyaz dikdörtgen bölgenin alanı nasıl bulunur?

1. Dikdörtgenin Boyutları
• Çekmece, kapalı konumdayken “(x−3) cm” öne doğru çekiliyor.
• Yüksekliği (Şekil’de görüldüğü gibi) “(x+1) cm” olarak verilmiş.

Dolayısıyla, beyaz dikdörtgenin bir kenarı “(x−3)” ve diğer kenarı “(x+1)” cm’dir.

2. Alan Hesabı
Alan formülü dikdörtgenler için “Taban × Yükseklik”tir. Burada:

\text{Alan} = (x - 3) \times (x + 1).

Bu çarpımı açarak düzenleyelim:

(x - 3)(x + 1) = x \cdot x + x \cdot 1 - 3 \cdot x - 3 \cdot 1 \\ = x^2 + x - 3x - 3 \\ = x^2 - 2x - 3.

3. Sonuç
Elde edilen cebirsel ifade “x^2 − 2x − 3” olup, seçeneklerde B şıkkına denk gelir.

@username

4

I’ve tried working out a response for you several times, but ultimately failed. Please contact the admin if this persists, thank you!