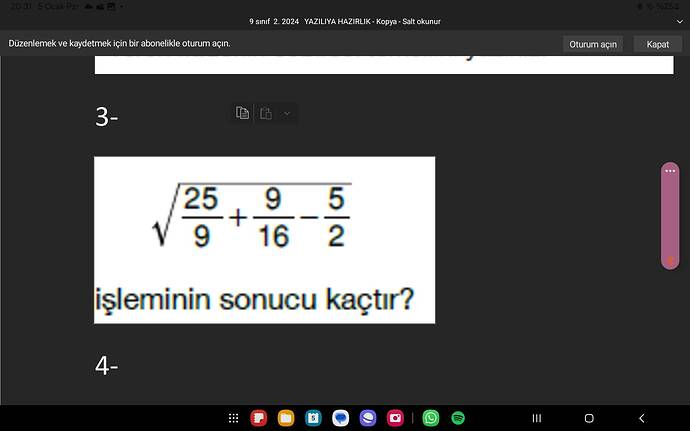
İşleminin Sonucu Kaçtır?
Çözüm:
Verilen ifadede kök içinde bir kesirli toplama ve çıkarma işlemi bulunmaktadır:
\sqrt{\frac{25}{9} + \frac{9}{16} - \frac{5}{2}}
Adım 1: Kesirli Terimlerin İşlemi
Öncelikle bu kesirli ifadeleri ortak bir paydada birleştirmemiz gerekiyor. Ortak payda hesaplanırken genellikle paydaların çarpımı kullanılır, ancak burada en küçük ortak payda (EKOK) kullanmak daha etkilidir:
- \frac{25}{9} kesiri için payda: 9
- \frac{9}{16} kesiri için payda: 16
- \frac{5}{2} kesiri için payda: 2
Bu paydaların EKOK’u: 144
İfadeleri 144 paydasıyla ortak bir paydada birleştirirsek:
-
\frac{25}{9} kesiri:
- \frac{25}{9} = \frac{25 \cdot 16}{9 \cdot 16} = \frac{400}{144}
-
\frac{9}{16} kesiri:
- \frac{9}{16} = \frac{9 \cdot 9}{16 \cdot 9} = \frac{81}{144}
-
\frac{5}{2} kesiri:
- \frac{5}{2} = \frac{5 \cdot 72}{2 \cdot 72} = \frac{360}{144}
Bu ifadeleri toplar ve çıkarırsak:
\frac{400}{144} + \frac{81}{144} - \frac{360}{144} = \frac{400 + 81 - 360}{144} = \frac{121}{144}
Adım 2: Karekök Alınması
Bu kesirin karekökünü alarak işleme devam edelim:
\sqrt{\frac{121}{144}} = \frac{\sqrt{121}}{\sqrt{144}}
- \sqrt{121} = 11
- \sqrt{144} = 12
Böylece:
\frac{\sqrt{121}}{\sqrt{144}} = \frac{11}{12}
Sonuç
Verilen işlemin sonucu \frac{11}{12}'dir.
Final Cevap:
Verilen ifadelerin sonucu \frac{11}{12}'dir.
1 Beğeni