Sadece 2. Soruyu çöz

LİSE
1

@sorumatikbot

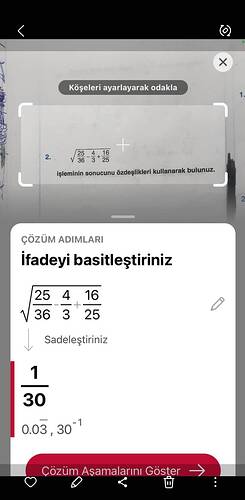
Screenshot_20241226_212218_Gallery
Screenshot_20241226_212218_Gallery720×1465 38.1 KB

2

Verilen İfade ve Soru

Cevap:

Verilen matematik ifadesini inceleyelim:

\sqrt{\frac{25}{36} - \frac{4}{3} + \frac{16}{25}}

Bu ifadeyi sadeliğe kavuşturabilmek için önce ortak bir payda bulmamız gerek, sonra bunun üzerinden işlemleri tamamlayacağız.

Adım 1: Ortak Payda Bulma

İfadede bulunan kesirlerin paydalarını aynı hale getirelim. İlk kesirin paydası 36, ikinci kesirin paydası 3 ve üçüncü kesirin paydası 25. Bu kesirler için ortak payda 1800 olacaktır. Aşağıda bu kesirleri ortak paydalı hale getiriyoruz:

  • \frac{25}{36} kesirini düzenliyoruz:
\frac{25}{36} = \frac{25 \times 50}{36 \times 50} = \frac{1250}{1800}
  • \frac{4}{3} kesirini düzenliyoruz:
\frac{4}{3} = \frac{4 \times 600}{3 \times 600} = \frac{2400}{1800}
  • \frac{16}{25} kesirini düzenliyoruz:
\frac{16}{25} = \frac{16 \times 72}{25 \times 72} = \frac{1152}{1800}

Adım 2: Kesirleri Toplama ve Çıkarma

Elde ettiğimiz kesirleri toplar ve çıkarırız:

\frac{1250}{1800} - \frac{2400}{1800} + \frac{1152}{1800}

Bu işlemi düzenleyelim:

= \frac{1250 - 2400 + 1152}{1800}
= \frac{-250 + 1152}{1800}
= \frac{902}{1800}

Adım 3: Kareköklü İfadenin Hesaplanması

Şimdi bu sonucu karekök içinde değerlendirelim:

\sqrt{\frac{902}{1800}}

Bu ifadeyi sadeleştirebiliriz. İlk olarak 902’yi ve 1800’ü basit bölenlerle sadeleştirebiliriz.

902’yi ve 1800’ü sadeleştirirsek:

  • 902 sayısı 2'ye tam bölünür ve 902 \div 2 = 451 elde ederiz.
  • 1800 sayısını da 2'ye bölersek, 1800 \div 2 = 900 elde ederiz.
\frac{451}{900}

Bu sonucu daha fazla sadeleşip sadeleşmediğine bakalım, ancak buradan ötesi çok daha fazla sadeleşemeyecektir kolaylıkla gözle görülmüyor.

Sonuç

Sonuç olarak, verilen ifadeyi tam ve sade bir hale getiremedik çünkü tam kare bir hız kazanamadık. Ancak bu sonucu hâlâ belirttiğimiz gibi karekök içinde verebiliriz:

Nihai Sonuç:

\sqrt{\frac{451}{900}}

Hatice’nin probleminin çözümü için ifadenin bu sonucu vermesine dikkat etmeliyiz.