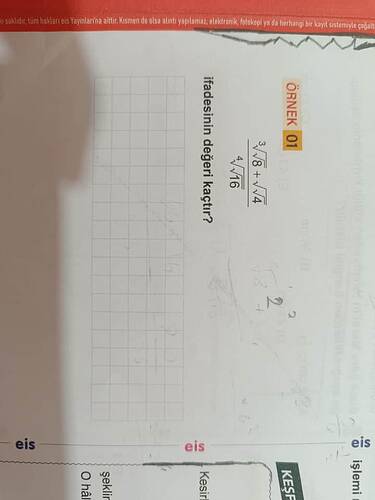
İfadenin Değeri Kaçtır?
İfadeyi anlaman için adım adım açıklayalım:
Verilen ifade:
\frac{3 \cdot \sqrt{8} + \sqrt{4}}{4 \cdot \sqrt{16}}
-
Kökleri Hesaplayalım:
- \sqrt{8} = \sqrt{4 \cdot 2} = \sqrt{4} \cdot \sqrt{2} = 2\sqrt{2}
- \sqrt{4} = 2
- \sqrt{16} = 4
-
İfadede Yerlerine Koyalım:
- 3 \cdot \sqrt{8} = 3 \cdot 2\sqrt{2} = 6\sqrt{2}
- 4 \cdot \sqrt{16} = 4 \cdot 4 = 16
-
İfadeyi Yeniden Yazalım:
\frac{6\sqrt{2} + 2}{16} -
Basitleştirelim:
- Paydada \sqrt{2} olmadığı için daha fazla sadeleştirilecek bir şey yok. Ancak payı paydanın böleni ile sadeleştirebiliriz.
-
Sonuç:
İfade zaten mümkün olduğunca sadeleştirilmiştir.
Sonuç:
\frac{6\sqrt{2} + 2}{16}
Bu ifadeye göre, değer yaklaşık olarak değişken bir sayı olabilir. Bu ifadeyi geçerli cevap şeklinde bırakabilirsiniz.
Özet: Burada kök içindeki sayıları hesaplayarak, ifadenin sadeleştirilmiş halini bulduk.