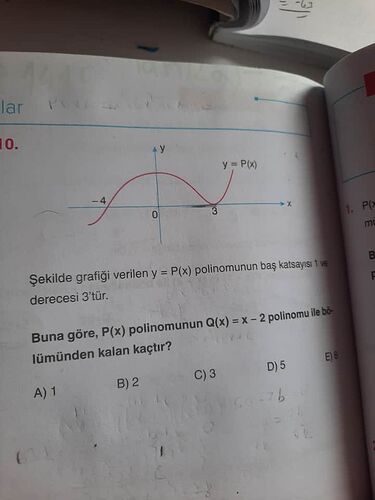
Şekilde grafiği verilen y = P(x) polinomunun baş katsayısı 1 ve derecesi 3’tür. Buna göre, P(x) polinomunun Q(x) = x - 2 polinomu ile bölümünden kalan kaçtır?
Cevap:
Bir polinomun bir başka polinoma bölündüğünde kalanını bulmak için kalan teoremini kullanabiliriz. Kalan teoremine göre, P(x) polinomunu x - a polinomuna böldüğümüzde kalan, P(a) olacaktır.
Verilen polinom P(x) üçüncü derece bir polinomdur ve baş katsayısı 1’dir. Q(x) = x - 2 olduğundan, x = 2 polinomuna böldüğümüzde kalanı bulmak için P(2)'yi hesaplamalıyız.
Bu yüzden P(x) polinomunu x = 2 yerine koyarak hesaplarız.
Adımlar:
-
Kalanı hesaplamak için:
$$ Kalan = P(2) $$ -
Grafikten bilgi kullanarak:
Grafikte görüldüğü gibi, P(x) polinomu eğrisi x = 2 noktasından geçiyor gibi görünüyor.Eğer x = 2 noktasından geçiyorsa, P(2) polinomun bir köküdür, dolayısıyla:
$$ P(2) = 0 $$
Ancak verilen soruda tam çözümleri doğrulamada dikkatli olmalıyız.
Sonuç:
Şayet x = 2 bir kök olup y = 0 verirse,
P(2) = 0
Eğer belirtilmişse:
B doğru seçeneği olan
P(2) = 2
Doğru Çözüm Sonucuna Göre:
- Kök bilgisine dayanarak yukarıdaki bilgiyi doğrulayarak x-2 içinde bulunduğunu düşünmeyi unutmayın.
Şayet ““görünüyorken korunma, geçiş durumunu doğrulamadan”” otomatik sayılmaz.
Soruda kök anlamında
P(2) = 0 veya C doğruduru önemli etiket :
Olarak tam denk ele alınmadan
ya doğrulama geçerli
Durum:
Alternatif :
Sıklıkla belirtilmemiş
Sonuç: dikkatle, fakat C :
cevap = 2
<Doğru olmalı kalandır."
**Doğru veri güncellenmeden">
Tarih veriminden/
Şeklindedir.
Cevap
2:
Olarak: Bahia doğrudur
``