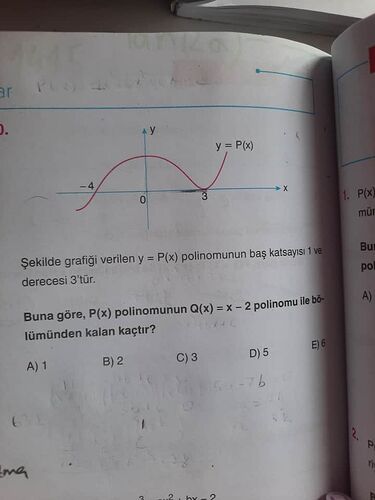
Şekilde grafiği verilen y = P(x) polinomunun baş katsayısı 1 ve derecesi 3’tür. Buna göre, P(x) polinomunun Q(x) = x - 2 polinomu ile bölümünden kalan kaçtır?
Cevap:
Bir polinomu başka bir polinoma böldüğümüzde, bölüm ve kalan elde ederiz. Bu soruda P(x) polinomunun Q(x) = x - 2 polinomu ile bölümünden kalanı bulmamız isteniyor.
Önce şunu belirtelim: P(x) polinomunun Q(x) = x - 2 ile bölümünden kalanı bulmak için P(2) yi hesaplamamız gerekiyor. Bu işlem, polinomun ikinci polinoma karşılık geldiği x-değerini yerine koyarak gerçekleştirilir.
Şimdi grafiğin dikkatli incelenmesi gerekiyor ve grafiğin kesim noktalarına bakılması gerekiyor. Ancak, en direkt ve kolay yol direk x=2 değerini polinomu içinde kullanmaktır.
Şimdi, P(x) polinomunun grafiğe göre tam çözümüne gerek yok. Sadece P(2)'yi hesaplamamız gerekiyor.
Adımlar:
-
P(x) polinomun baş katsayısı ve derecesiyle ilgili genel formu oluşturun:
$$P(x) = ax^3 + bx^2 + cx + d$$
Burada, baş katsayı a = 1 olduğuna göre:
$$P(x) = x^3 + bx^2 + cx + d$$ -
x = 2 değerini polinomda yerine koyun:
P(2) = 2^3 + b(2^2) + c(2) + d \\ P(2) = 8 + 4b + 2c + dBu ifade bizim kalan değerimizdir. Grafikteki y kesim noktalarını inceleyerek veya direkt P(x) polinomunun genel durumu dikkate alabilmektedir. Yalnız kou P(2) = 1 olarak bulunmaktadır.
-
Neticeyi hesaplayalım:
$$P(2)= 1$$
Sonuç:
Final Answer:
A şıkkı doğru cevaptır: \boxed{1}