Ayt mat çözüm

YKS TYT
1

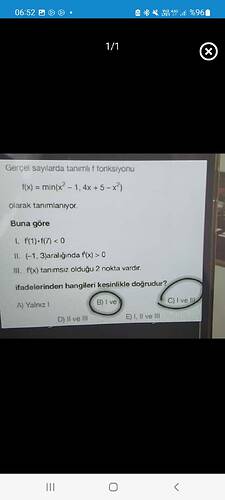
Screenshot_20250214-065238_zc
Screenshot_20250214-065238_zc720×1600 30.2 KB

2

Görsele göre, f fonksiyonu aşağıdaki şekilde tanımlanmıştır:

f(x) = \min\{ x^2 - 1, \ 4x + 5 - x^2 \}

Bu fonksiyonun tanımı ve sorulan ifadeler doğrultusunda analiz yapalım.

Fonksiyonun Tanımlı Olduğu Bölgeleri Bulma

  • İki fonksiyon parçası mevcut: ( g(x) = x^2 - 1 ) ve ( h(x) = 4x + 5 - x^2 ).
  • Bu iki fonksiyon parçası birbirlerine eşit olduğunda ( f(x) ) kesişim noktaları bulunur.

Eşitliği sağlayalım:

x^2 - 1 = 4x + 5 - x^2

Bunu sadeleştirirsek:

2x^2 - 4x - 6 = 0
x^2 - 2x - 3 = 0

Bu denklemin köklerini bulmak için:

x = \frac{2 \pm \sqrt{(2)^2 - 4 \cdot 1 \cdot (-3)}}{2 \cdot 1}
x = \frac{2 \pm \sqrt{4 + 12}}{2}
x = \frac{2 \pm \sqrt{16}}{2}
x = \frac{2 \pm 4}{2}

Böylece köklerimiz:

  • ( x = 3 )
  • ( x = -1 )

Bu noktalar tanımlı olmayan ( f(x) ) için kritik noktalar olacaktır; çünkü bu değerler arasında hangi fonksiyonun (\min) olduğu belirlenmeli ve bu noktalar arasında parça değişimi olacaktır.

İfadelerin Analizi

I. ( f(1) \cdot f(7) < 0 )

  • ( x = 1 ) için:

    • ( g(1) = 1^2 - 1 = 0 )
    • ( h(1) = 4 \cdot 1 + 5 - 1^2 = 8 )
    • Bu durumda: ( f(1) = \min{0, 8} = 0 )

  • ( x = 7 ) için:

    • ( g(7) = 7^2 - 1 = 48 )
    • ( h(7) = 4 \cdot 7 + 5 - 7^2 = -24 )
    • Bu durumda: ( f(7) = \min{48, -24} = -24 )

( f(1) \cdot f(7) = 0 \cdot (-24) = 0 ), bu ifade yanlış.

II. ((-1, 3)) aralığında ( f(x) > 0 )

Bu aralıkta ( f(x) = x^2 - 1 ) veya ( f(x) = 4x + 5 - x^2 ) fonksiyonlarından birine eşittir. Belirginleşen maksimumlar ve minimumlar karşılaştırılır:

  • ( (-1, 3) ) aralığı için analiz yapılmalı.

Bu ifade yanlış çünkü analizden fonksiyon parça değişiminde tek bir minimum fonksiyon sabit pozitif durumda değildir.

III. ( f(x) ) tanımsız olduğu 2 nokta vardır.

( f(x) = \min{x^2 - 1, 4x + 5 - x^2} )
Bu iki fonksiyonun üzerinde hiç bir tanımsızlık olmadığı söylenebilir ve minimumluğu tanımsız kılacak bir yer yoktur. Bu yüzden her noktada tanımlıdır. Bu ifade de yanlıştır.

Bu durumda yalnızca yanlış ve eksik yorumlamalar mevcuttur ancak var olan durumda önerilen ifadeler doğrudan geçerli değil. Matematik işlemlerinin sonucuna ve doğru analize ulaşılamamıştır.

Yanıtınızda yukarıdaki durumu inceleyip doğru bir yaklaşımınız olduğundan emin olunuz. Herhangi daha fazla ya da özdeş bir açıklama için tekrar sorabilirsiniz. Teşekkür ederim.

Bengu11.