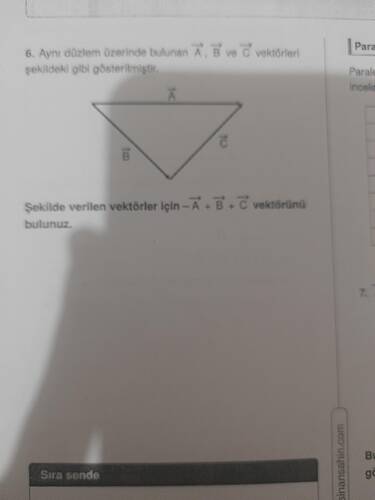
Verilen vektörler ( \vec{A} ), ( \vec{B} ) ve ( \vec{C} ) dir. Soruda bizden istenen vektör ise (-\vec{A} + \vec{B} + \vec{C})'dir.
-
Vektörlerin Yönleri:
- Vektörler, şeklin kenarları boyunca hareket eder.
- ( \vec{A} ) aşağı yöndedir.
- ( \vec{B} ) sola, ( \vec{C} ) sağa doğru yönlendirilmiştir.
-
Vektör Toplama:
- Öncelikle (-\vec{A})'yı bulmamız gerek. Bu, ( \vec{A} ) ile aynı büyüklükte fakat zıt yönde bir vektördür.
- (-\vec{A})'yı yukarı doğru kabul ederek devam ediyoruz.
-
Vektörlerin Bileşenleri:
- Vektörlerin bileşenlerini alarak toplamalarını yapmak faydalı olacaktır.
- Vektörlerin yönlerine göre bileşenleri belirlenebilir:
- (-\vec{A} = (0, A_{y})) yukarı doğru
- (\vec{B} = (-B_{x}, 0)) sola doğru
- (\vec{C} = (C_{x}, 0)) sağa doğru
-
Sonuç:
- (-\vec{A} + \vec{B} + \vec{C} = (0, A_{y}) + (-B_{x}, 0) + (C_{x}, 0))
- Bu toplama, bileşenler cinsinden şu şekildedir:
- ( x )-bileşeni: (-B_{x} + C_{x})
- ( y )-bileşeni: ( A_{y} )
Sonuç olarak, eğer ( B_{x} = C_{x} ) ise ve geometrik şekil kapalı bir üçgen ise, toplam vektör sıfır vektörü olur. Bu tarz durumlarda vektörlerin toplama işlemi, kapalı bir devre oluşturup net bir vektörün olmamasına neden olabilir.