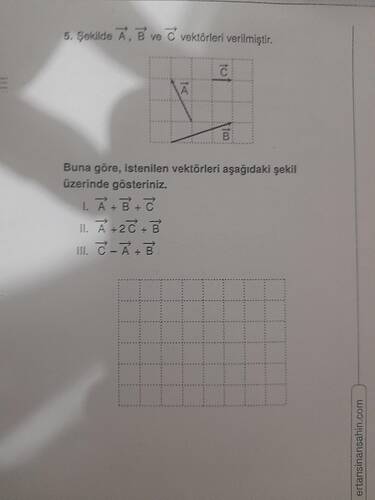
Görselde üç adet vektör verilmiş ve bu vektörlerle bazı işlemler yapılması isteniyor. İşlemleri sırayla ele alalım:
-
( \vec{A} + \vec{B} + \vec{C} ):
- Öncelikle ( \vec{A} ) ve ( \vec{B} ) vektörlerini uç uca ekleyip toplamı bulalım. Vektörlerde birleştirme yaparken, bir vektörün ucunu diğerinin başlangıç noktasıyla birleştiriyoruz.
- Daha sonra ( \vec{C} ) vektörünü de ekleyerek sonucu elde ediyoruz.
- Bu işlem bittikten sonra toplam vektörü yeni bir başlangıç noktası alarak çizebiliriz.
-
( \vec{A} + 2 \cdot \vec{C} + \vec{B} ):
- Bu adımda ( \vec{C} ) vektörünü iki katına çıkarıyoruz. Bunun anlamı, ( \vec{C} ) vektörünü, aynı yönde olacak şekilde iki kez eklemektir.
- Öncelikle ( \vec{A} ) vektörünü çizin, ardından ( 2 \cdot \vec{C} ) vektörünü uç uca ekleyin.
- Son olarak ( \vec{B} ) vektörünü ekleyerek toplam vektörü tamamlayın.
-
( \vec{C} - \vec{A} + \vec{B} ):
- Burada ( -\vec{A} ) vektörü, ( \vec{A} ) vektörünün yönünün ters çevrilmiş halidir.
- Önce ( \vec{C} ) vektörünü çizin, ardından ( -\vec{A} ) vektörünü ekleyin. Bu, ( \vec{A} ) vektörünün tersini alarak yapılır.
- Sonrasında ( \vec{B} ) vektörünü ekleyin.
Her bir işlem sonunda elde ettiğiniz toplam vektörü ayrı ayrı çizmenin, verilen şekil üzerinde anlamlı bir şekilde gösterilmesi beklenmektedir. Vektörlerin başlangıç noktasından başlayan ve uçlarına doğru devam eden yeni çizimleri yaparak sorunun çözümünü tamamlayabilirsiniz.