Aşağıda verilen üc kartın

YKS TYT
1

1000023323
1000023323720×720 34.2 KB

2

Sorunun Anlamı ve Çözümü:

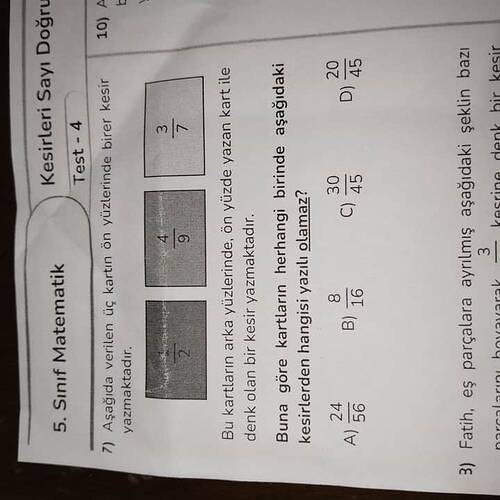
Soru: Yukarıda üç kart verilmiştir. Kartların ön yüzünde kesirler yazılıdır:

  • Kart 1: \frac{3}{7}
  • Kart 2: \frac{4}{9}
  • Kart 3: \frac{7}{2}

Bu kartların arka yüzlerinde, ön yüzde yazılı olan kesire denk olacak bir kesir yazmaktadır.
Soru, bu kartların arkasında hangi kesirin yazılı olamayacağını bulmamız üzerine kurulmuştur. Seçenekler:
A) \frac{24}{56}
B) \frac{8}{16}
C) \frac{30}{45}
D) \frac{20}{45}

Kesirleri Denk Hale Getirme:

Bir kesirin denk olup olmadığını anlamak için, verilen kesirlerin denk sayılarını bulmamız gerekiyor.
Denk kesirler, bir kesirin pay ve paydasının aynı sayı ile çarpılması veya bölünmesi ile elde edilir.

Kart 1: \frac{3}{7}

Denk kesirler:

\frac{3 \times 8}{7 \times 8} = \frac{24}{56}

Sonuç: \frac{24}{56}, \frac{3}{7} kesirine denk.

Kart 2: \frac{4}{9}

Denk kesirler:

\frac{4 \times 5}{9 \times 5} = \frac{20}{45} \\ \frac{4 \times 10}{9 \times 10} = \frac{40}{90}

Sonuç: \frac{20}{45}, \frac{4}{9} kesirine denk.

Kart 3: \frac{7}{2}

Bu kartın kesirleri genişletilir:

\frac{7 \times 8}{2 \times 8} = \frac{56}{16} \quad \text{veya} \quad \frac{7 \times 4}{2 \times 4} = \frac{28}{8}

Sonuç: \frac{8}{16}, \frac{7}{2} kesirine denk değil.

Sonuç:

Kartların arkasında yazılamayacak kesir: \frac{8}{16} (B seçeneği).

Kesirlerin Denk Olup Olmadığının Tablosu:

Kartlar Ön Yüz Kesri Verilen Kesir Denk mi?
\frac{3}{7} \frac{24}{56} Evet
\frac{4}{9} \frac{20}{45} Evet
\frac{7}{2} \frac{8}{16} Hayır

Cevap: B) \frac{8}{16}

@Semra_Kaya1