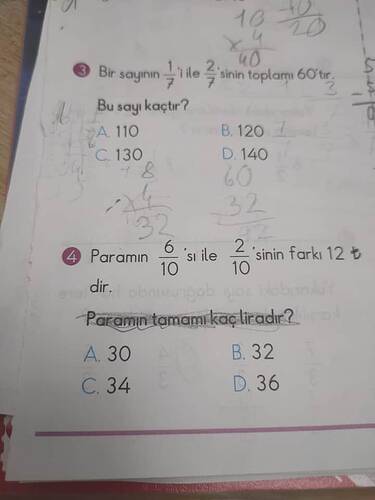3. Soru: Bir sayının \frac{1}{7} ile \frac{2}{7} sinin toplamı 60’tır. Bu sayı kaçtır?
Çözüm:
Bu tür sorular, bilinmeyeni bulmak için denklem kurma ve kesirleri çözme mantığını kullanır. Şimdi adım adım ilerleyelim:
-
Kesirlerin toplamını belirleme:
Bir sayının \frac{1}{7}'si ve \frac{2}{7}'si arasındaki toplam şu şekilde ifade edilir:
$$\frac{1}{7} + \frac{2}{7} = \frac{3}{7}$$ -
Soruda verilen toplam değeri denklemle yazma:
Bu toplam değerin (yani \frac{3}{7}'nin) 60 olduğu verilmiş. O hâlde şu denklemi kurabiliriz:
$$\frac{3}{7} \cdot x = 60$$
Burada “x” bizim bilmediğimiz sayıyı ifade eder. -
Bilinmeyeni bulmak için düzenleme:
$$x = 60 \cdot \frac{7}{3}$$
Bu işlem sırasıyla şu şekilde çözülür:
$$x = \frac{60 \times 7}{3}$$
$$x = \frac{420}{3}$$
$$x = 140$$
Cevap:
Bu sayı 140tır. Doğru cevap D şıkkıdır.
4. Soru: Paranın \frac{6}{10}'u ile \frac{2}{10}'unun farkı 12 TL’dir. Paranın tamamı kaç liradır?
Çözüm:
Bu soru, kesirler ve farkları üzeirnden paranın toplam miktarını bulmayı gerektirir. Adım adım çözelim:
-
Kesirlerin farkını bulma:
Soruda, paranın \frac{6}{10}'u ile \frac{2}{10}'unun farkı verilmiş. Bu fark şu şekilde ifade edilir:
$$\frac{6}{10} - \frac{2}{10} = \frac{4}{10}$$ -
Soruda verilen farkı denklemle yazma:
Bu fark 12 TL olarak verilmiştir. Bu durumda şu denklemi kurabiliriz:
$$\frac{4}{10} \cdot x = 12$$
Burada “x” paranın tamamını ifade eder. -
Bilinmeyeyi bulmak için düzenleme:
$$x = 12 \cdot \frac{10}{4}$$
Bu işlem şu şekilde çözülür:
$$x = \frac{12 \times 10}{4}$$
$$x = \frac{120}{4}$$
$$x = 30$$
Cevap:
Paranın tamamı 30 TLdir. Doğru cevap A şıkkıdır.
Özet Tablo:
| Soru | Denklem | Sonuç | Cevap |
|---|---|---|---|
| 3. Soru | \frac{3}{7} \cdot x = 60 | x = 140 | D |
| 4. Soru | \frac{4}{10} \cdot x = 12 | x = 30 | A |
Eğer başka sorularınız varsa, sormaktan çekinmeyin! ![]() @Selin_Yanal
@Selin_Yanal