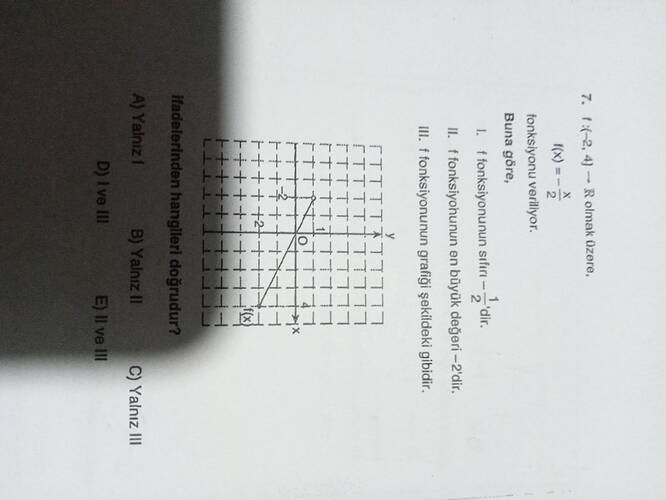
Görselde verilen fonksiyon sorusunu inceleyelim:
Fonksiyon Tanımı:
Fonksiyon ( f(x) = -\frac{x}{2} ) olarak verilmiş. Fonksiyonun tanım aralığı ([-2, 4]) ve değer kümesi ( \mathbb{R} ) olarak belirtilmiş.
İfadelerin Analizi:
-
I. Fonksiyonun sıfırı (-1)'dir.
- Bir fonksiyonun sıfırı, ( f(x) = 0 ) eşitliğini sağladığı ( x ) değeridir.
- ( f(x) = 0 ) için:
[
-\frac{x}{2} = 0 \implies x = 0
] - Dolayısıyla, fonksiyonun sıfırı (0)'dır, (-1) değildir. Bu ifade yanlıştır.
-
II. Fonksiyonun en büyük değeri (-2)'dir.
- Fonksiyonun tanım aralığı ([-2, 4]) olduğuna göre, bu aralıkta uç noktalar ve varsa kritik noktalar incelenmelidir.
- ( x = -2 ) olduğunda:
[
f(-2) = -\frac{-2}{2} = 1
] - ( x = 4 ) olduğunda:
[
f(4) = -\frac{4}{2} = -2
] - Bu aralıktaki en büyük değer (1)'dir, (-2) değildir. Bu ifade yanlıştır.
-
III. Fonksiyonun grafiği şekildeki gibidir.
- Fonksiyon ( f(x) = -\frac{x}{2} ) doğru fonksiyonudur ve verilen şekilde bu doğrunun tanım aralığı ([-2, 4]) kapsamında çizildiği görülüyor.
- Bu ifade doğrudur.
Sonuç:
Doğru olan ifade yalnız III numaralı ifadedir.
Bu nedenle cevap C) Yalnız III olacaktır.