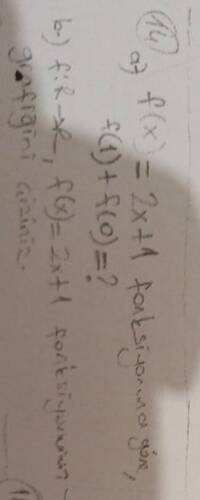Acilllllll düzgünn cevaplama

YKS TYT
1

IMG_20241226_185358
IMG_20241226_185358324×809 43 KB

2

Verilen Fonksiyonlar ve Grafiğini Çizme

Cevap:

Verilen soruda, bir fonksiyon ( f(x) = 2x + 1 ) olarak tanımlanmış. Bu fonksiyonun, belirli değerlere göre hesaplanması ve grafiğinin çizilmesi isteniyor. Soruyu adım adım inceleyelim.

Adım 1: Fonksiyon Değerlerini Bulma

a) Öncelikle, ( f(1) + f(0) ) ifadesini bulmamız gerekiyor.

  • ( f(x) = 2x + 1 ) fonksiyonunu kullanarak,
    • ( f(1) ) değerini bulalım:
      $$ f(1) = 2 \times 1 + 1 = 3 $$
    • ( f(0) ) değerini bulalım:
      $$ f(0) = 2 \times 0 + 1 = 1 $$

Buna göre,

  • ( f(1) + f(0) = 3 + 1 = 4 )

Adım 2: Fonksiyonun Grafiğini Çizme

b) Fonksiyonun grafiği çizilirken, ( f(x) = 2x + 1 ) doğrusunun grafiğini çizmemiz gerekiyor. Bu, y = mx + c formunda bir doğrudur, burada:

  • ( m = 2 ): Eğim
  • Yani, ( x ) eksenin bir birim sağa kaydığında, ( y ) iki birim yukarı çıkar.
  • ( c = 1 ): y eksenini kestiği nokta.

Grafik Çizimi İçin Öne Çıkan Noktalar:

  1. Başlangıç Noktası: (0,1) - (y eksenini kestiği nokta)
  2. Eğim Noktası: Her 1 birim sağa (pozitif x yönünde) hareket ettiğimizde, 2 birim yukarı (pozitif y yönünde) gideriz. Bu yüzden, ikinci bir nokta (1,3) olacaktır.
  3. Bu iki noktayı birleştirdiğimizde, ( f(x) = 2x + 1 ) doğrusu elde edilir.

Grafik Çizimi:

   |
 4 |        *
 3 |      *(1,3)
 2 |       |
 1 *-------|-----------  y Ekseni
   |(0,1)
---+------------------  X Ekseni
   |

Sonuç:

a) ( f(1) + f(0) = 4 ) olarak bulunmuştur.

b) Grafiği, ( f(x) = 2x + 1 ) doğrusu olarak çizilmiştir. Doğru y eksenini (0, 1) noktasında kesmekte ve her 1 birim sağa 2 birim yukarı çıkmak ile tanımlanmaktadır.

Son Cevap:

  • ( f(1) + f(0) = 4 )
  • Grafiği, ( y = 2x + 1 ) şeklinde bir doğrudur.