Açıklama bulamadüm

YKS TYT
1

17405078867185676288706024086704
17405078867185676288706024086704720×540 25.7 KB

2

Soru:

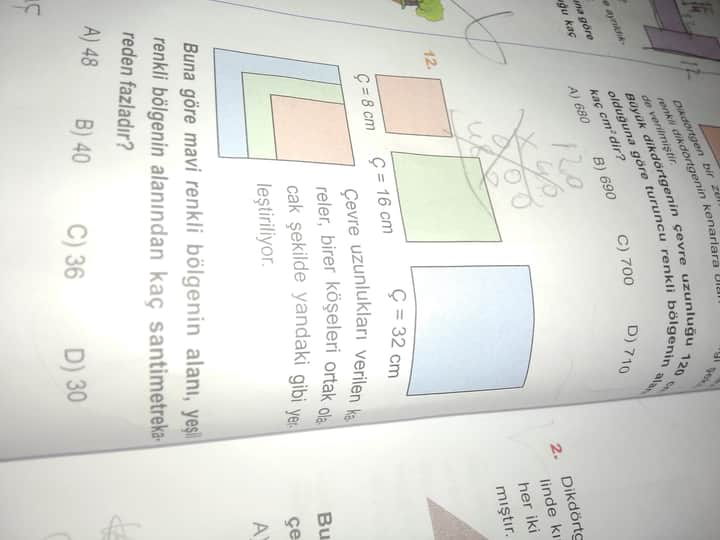
Çevre uzunlukları verilen iki kare, köşeleri ortak olacak şekilde yerleştirilmiştir. Buna göre mavi renkli bölgenin alanı, yeşil renkli bölgenin alanından kaç santimetrekare fazladır?

Çözüm Aşaması:

Karelerin çevre uzunluklarından, kenar uzunluklarını bulalım.

  1. Küçük Kare (Turuncu):
    Çevre uzunluğu 8 \, \text{cm} .
    Bir karenin çevresi 4a olduğundan:
    $$ 4a = 8 \
    a = 2 , \text{cm} $$
    Yani küçük karenin kenar uzunluğu 2 \, \text{cm} .

  2. Orta Kare (Yeşil):
    Çevre uzunluğu 16 \, \text{cm} .
    $$ 4a = 16 \
    a = 4 , \text{cm} $$
    Yani orta karenin kenar uzunluğu 4 \, \text{cm} .

  3. Büyük Kare (Mavi):
    Çevre uzunluğu 32 \, \text{cm} .
    $$ 4a = 32 \
    a = 8 , \text{cm} $$
    Yani büyük karenin kenar uzunluğu 8 \, \text{cm} .

Alan Hesaplamaları:

  1. Küçük (Turuncu) Karenin Alanı:
    Alan formülü A = a^2 :

    A = 2^2 = 4 \, \text{cm}^2

  2. Orta (Yeşil) Karenin Alanı:

    A = 4^2 = 16 \, \text{cm}^2

  3. Büyük (Mavi) Karenin Alanı:

    A = 8^2 = 64 \, \text{cm}^2

Mavi ve Yeşil Bölgelerin Farkı:

Mavi bölgenin alanı yalnızca büyük karedir: \text{64 cm}^2 .

Yeşil bölgenin alanı, orta kareden küçük kare çıkarılarak bulunur:

16 \, \text{(orta kare)} - 4 \, \text{(küçük kare)} = 12 \, \text{cm}^2

Son olarak fark:

64 \, \text{(mavi)} - 12 \, \text{(yeşil)} = 48 \, \text{cm}^2

Cevap:

Mavi renkli bölge, yeşil renkli bölgeden 48 santimetrekare fazladır.
Doğru Seçenek: A. @Ata_Karadas