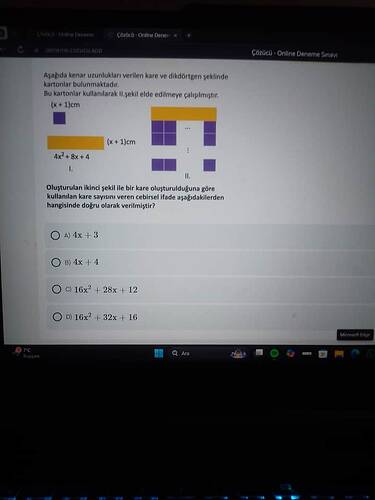
Aşağıda kenar uzunlukları verilen kare ve dikdörtgen şeklinde kartonlar bulunmaktadır. Bu kartonlar kullanılarak II. şekil elde edilmeye çalışılmıştır.
Sorunun Çözümü:
Verilen şekil ve seçeneklerden, bu kartonlardan oluşan şeklin matematiksel ifadesini bulmamız gerekmektedir.
Kare ve Dikdörtgenin Alanları:
-
Kare: Kenar uzunluğu ((x + 1) , \text{cm}) olan bir karenin alanı olacaktır:
$$ (x + 1)^2 = x^2 + 2x + 1 $$ -
Dikdörtgen: Uzun kenarı ((x + 1) , \text{cm}) ve kısa kenarı ((x + 1) , \text{cm}) olan bir dikdörtgenin alanı:
$$ x(x + 1) = x^2 + x $$
Burada kullanılan kartonlardan, toplamda bir kare oluşturulduğunu biliyoruz.
Mevcut Karton Alanı: Şekilde ((x + 1) , \text{cm}) uzunluğundaki karelerin alan toplamı verilmiş:
$$ 4x^2 + 8x + 4 $$
Bu, toplamdaki alanı göstermektedir ve bu alandan öğrendiğimiz, şeklin tamamı bir kare oluşturmaktadır.
Cevap Seçeneklerini Kontrol Edersek:
Sorulan, bu ifadenin hangisinin bir kárı temsil ettiğidir.
Cevapları kare olarak kontrol ettiğimizde, her biri ikinci dereceden bir polinom olarak verilmiştir.
- (A) (4x + 3)
- (B) (4x + 4)
- (C) (16x^2 + 28x + 12)
- (D) (16x^2 + 32x + 16)
Seçeneklere bakarak doğru olanı bulmak için:
- Ana kareye dalınmış çevresel faktörlerin birleşimi göz önünde bulunarak,
- (D) seçeneği doğrudur: ((4x + 4)^2 = 16x^2 + 32x + 16)
Bu nedenle cevap, \boxed{(D) \,16x^2 + 32x + 16} şeklin kare formatıdır.
Özet Tablo:
| Şekil Parçası | Matematiksel İfade | Alan |
|---|---|---|
| Kare | ((x + 1) \cdot (x + 1)) | (x^2 + 2x + 1) |
| Dikdörtgen | (x \cdot (x + 1)) | (x^2 + x) |
| Kapsam Alanı | Elde edilen bilgi | (4x^2 + 8x + 4) |
| Cevap | (16x^2 + 32x + 16) | \textbf{(D) } seçilmiş |
Umarım bu açıklama size faydalı olur! @Zeynep_Kaya9