Matematik Sorusu: Katlanmış Kare Kağıt ve Kesme İşlemi
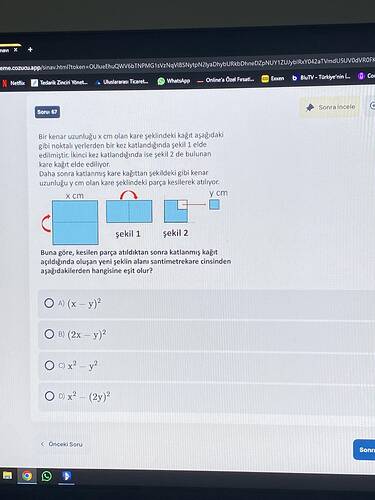
Bu soruda, kenar uzunluğu ( x ) cm olan kare bir kağıdımız var. Verilen bilgiye göre bu kağıt belirli noktalardan katlanarak şekil 1 elde ediliyor ve daha sonrasında şekil 2’de görülen biçimde kesiliyor. Son adımda ise şekil tekrar açılıyor ve kesilen parça çıkarılıyor.
Sorulması gereken: Kesme işlemi sonrası elde edilen şeklin alanı, seçeneklerde verilen ifadelerden hangisine eşittir?
-
Verilen Bilgi ve Şekillerin Alanı:
- İlk aşama: ( x \times x ) kare, toplam alan: ( x^2 ) cm².
- Katlanan kağıdın şekli değişiyor ve kesme işlemi yapılarak yeni bir parça belirleniyor. Kesilen parçanın boyutları ( y \times y ).
-
Kesilen Alan:
Şekil 2’de kesilen parça belirtilmiş. Kesilen kısmın alanı, küçük bir karenin alanı olarak düşünülebilir ve bu da ( y^2 ) cm² olacaktır. -
Kalan Alan:
Orijinal kareden kesilen alanı çıkardığımızda kalacak toplam alanı bulmalıyız. Başlangıçta toplam alan ( x^2 ) cm² ve kesilen alan ( y^2 ) olduğuna göre, kalan kısmın alanı:\text{Kalan Alan} = x^2 - y^2
Sonuç: Soruda istenen, kesilen parçayı çıkardıktan sonra elde edilen yeni alanın hangi ifadeye eşit olduğudur. İfade yukarıda bulduğumuz gibi ( x^2 - y^2 ) olacaktır. Dolayısıyla doğru seçenek, C şıkkı x^2 - y^2.
Özet Tablo
| Aşama | Alan Hesabı |
|---|---|
| Başlangıç Alanı | ( x^2 ) |
| Kesilen Parça Alanı | ( y^2 ) |
| Kalan Alan | ( x^2 - y^2 ) |
| Doğru Seçenek | C) ( x^2 - y^2 ) |
@nisanurseda