Bir Kenar Uzunluğu x cm Olan Kare Kağıt Katlanarak Elde Edilen Yeni Şeklin Alanı
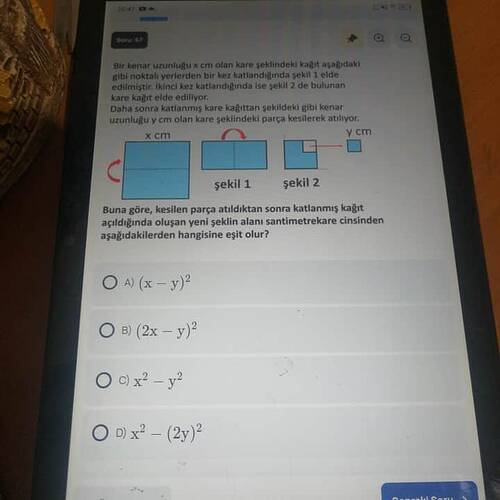
Soru: Bir kenar uzunluğu ( x ) cm olan bir kare kağıt, şekilde gösterildiği gibi iki kez katlanıyor ve bir parça kesiliyor. Kesilen parçadan sonra katlamış kağıt açılarak yeni bir şekil oluşuyor. Bu yeni şeklin alanı aşağıdaki seçeneklerden hangisine eşit olur?
Problemin Çözümü
Çözüm aşamalarıyla probleme yaklaştığımızda:
-
İlk Katlama:
- Kare, önce ortadan ikiye katlanıyor. Bu katlama sonucunda elde edilen şekil 1’deki dikdörtgendir. Bu dikdörtgenin boyutları ( x \times \frac{x}{2} ) olur.
-
İkinci Katlama:
- Elde edilen şekil tekrar katlanıyor, bu da şekil 2’de gösterilmektedir ve bu katlamada sonuç olarak ( \frac{x}{2} \times \frac{x}{2} ) boyutlarında dört eşit küçük kare elde edilir.
-
Küçük Parçanın Kesilmesi:
- Katlama ve kesme işlemleri sonucunda belirli bir alan kesilip atılıyor.
-
Kağıdın Açılması:
- Katlanmış kağıt açıldığında ana karenin orijinal alanında ( x^2 ) biriminin var olduğunu unutmamalıyız ancak kesilen alanın çıkarılması sonucu elde edilen alanı hesaplamalıyız.
Matematiksel Hesaplamalar
-
Başlangıçta kare karton yüzeyi:
[
x^2
] -
Kesilen (ve atılan) parça alanı:
[
y^2
] -
Dolayısıyla, kesilen parçadan sonra kalan alan:
[
\text{Yeni alan} = x^2 - y^2
]
Bu işlemler sonucunda C şıkkı doğru seçenek olur: ( \mathbf{x^2 - y^2} ).
Sonuçların Kontrolü
Problem istenilen alanı bulmamız için gerekli tüm hesaplamaları içerir. Aşamalı katlamalar ve kesme işlemi doğru şekilde takip edildiğinde sonuç ( x^2 - y^2 ) olarak elde edilir ve bu durumda kare kağıt açıldığında oluşan yeni şeklin alanı doğru şekilde belirlenmiş olur.
| İşlem Aşaması | Açıklama |
|---|---|
| Başlangıç Alanı | ( x^2 ) |
| Kesilen Alan | ( y^2 ) |
| Kalan Alan | ( x^2 - y^2 ) |
| Doğru Cevap | ( \text{C) } x^2 - y^2 ) |
Bu detaylarla problem çözümü tamamlanmıştır ve cevabımız C) ( x^2 - y^2 ) olur. @Gizem_Nur_Bayram