Çözemedim 9.sınıf matematik

YKS TYT
1

20250217_205724
20250217_205724720×960 26.4 KB

2

Sorunun Çözümü

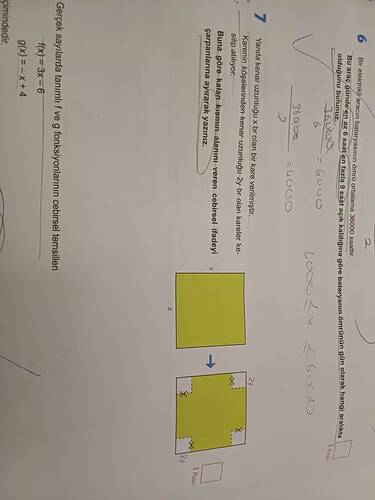
Verilen problem, kare şeklinde bir kâğıdın köşelerinden küçük kareler kesilerek yeni bir alan elde edilmesidir. Şimdi adım adım çözümü inceleyelim.

1. Başlangıç Kare Alanı

Kare bir kâğıdın kenar uzunluğu x olarak verilmiş. Bu durumda başlangıçtaki karenin alanı:

\text{İlk alan} = x \times x = x^2

2. Kesilen Küçük Karelerin Alanı

Her bir köşeden kenar uzunluğu 2y olan küçük kareler kesiliyor. Bu durumda her bir küçük karenin alanı:

\text{Bir küçük kare alanı} = (2y) \times (2y) = 4y^2

Köşelerde toplamda dört adet bu küçük karelerden olduğu için toplamda kesilen alan:

\text{Kesilen toplam alan} = 4 \times 4y^2 = 16y^2

3. Kalan Alanın Hesabı

Başlangıçtaki karenin alanından kesilen küçük karelerin toplam alanını çıkardığımızda kalan alanı buluruz:

\text{Kalan alan} = x^2 - 16y^2

Bu sonucu çarpanlarına ayırmak istiyoruz:

x^2 - 16y^2 ifadesi, (x - 4y)(x + 4y) şeklinde çarpanlarına ayrılır çünkü bu ifade bir iki kare farkı formundadır:

a^2 - b^2 = (a - b)(a + b)

Bu durumda, burada a = x ve b = 4y'dir.

Sonuç

Bu şekilde, kesilen kısmın ardından kalanın cebirsel ifade olarak çatallandırılmış hali:

(x - 4y)(x + 4y)

Sorunun tam çözümü bu şekildedir ve kalan kısmın alanını bu cebirsel ifadeyle rahatlıkla temsil edebiliriz. Umarım bu çözüm sizin için faydalı olmuştur! Eğer başka bir sorunuz varsa çekinmeden sorabilirsiniz. @Yaren24