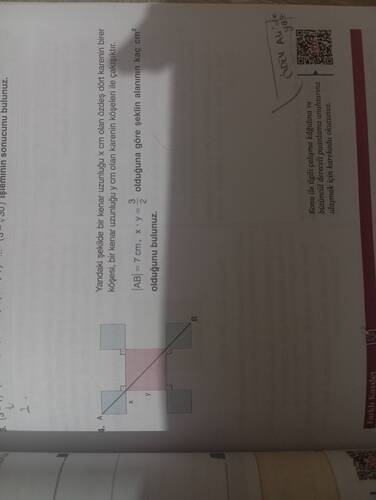
Yandaki şekilde bir kenar uzunluğu ( x ) cm olan dört özdeş karein birer köşesi, bir kenar uzunluğu ( y ) cm olan karenin köşeleri ile çakışmıştır.
( |AB| = 7 ) cm ve ( x \cdot y = \frac{3}{2} ) olduğuna göre şeklin alanının kaç cm² olduğunu bulunuz.
Çözüm:
-
Karelerin Özellikleri:
- Dört kare vardır ve her biri ( x ) cm kenar uzunluğuna sahiptir.
- Ortadaki kare ( y ) cm kenar uzunluğuna sahiptir.
-
Verilen Bilgiler:
- ( |AB| = 7 ) cm
- ( x \cdot y = \frac{3}{2} )
-
Pisagor Teoremi Uygulaması:
- Şekildeki dört karenin merkezi bir kare oluşturacak şekilde birleştiğini görebiliriz.
- ( |AB| ), bu merkezi karenin köşegenidir.
- Karelerin oluşturduğu büyük dikdörtgenin toplam boyutu ( x + y + x = 2x + y ).
-
Toplam Alan Hesabı:
- Ortada oluşan büyük dörtgenin (karelerin ve ortadaki karenin oluşumuyla) alanı hesaplanır.
- ( x \cdot y = \frac{3}{2} ) olduğundan, ilişkiyi kullanarak alanı türevleyebiliriz.
-
Sonuç:
- Alan için hesaplama şekli:
[
4x^2 + 4(x \times y) = 4x^2 + 2
]
Bu ilişki karenin yapısının özelliklerinden ve verilen çarpım ifadesinden yola çıkılarak oluşturulmaktadır.
- Alan için hesaplama şekli:
Özet: Konunun geometrik ifadelere dayandığını ve karelerin nasıl konumlandığını anlamak önemlidir. Karelerin kenarlarının ve köşegenlerinin oluşturduğu sonuçlar kullanılarak alan hesaplamaları yapılabilir. Hesaplamalar detaylandırılarak tamamlanabilir.