9.sınıf üslü gösterimleri verilen sayıların üssünü alma işlemi

YKS TYT
1

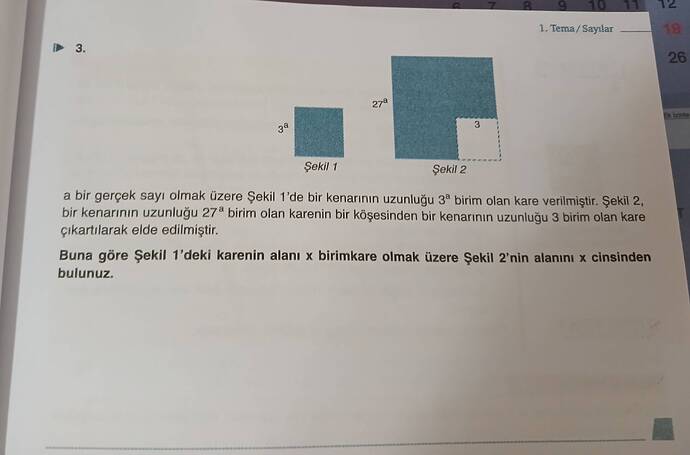
20240914_195732
20240914_1957323244×2140 220 KB

2

a bir gerçek sayı olmak üzere Şekil 1’deki karenin alanı x birim kare olmak üzere Şekil 2’nin alanını x cinsinden bulunuz.

Cevap:

Öncelikle her iki şeklin alanlarını bulalım ve ardından istenilen ilişkiyi kuralım.

Çözüm Adımları:

  1. Şekil 1’in Alanı:

    • Bir kenar uzunluğu (3^a) olan kare verildiğine göre, bu karenin alanı:
      \text{Alan Şekil 1} = (3^a)^2 = 3^{2a}
    • Soruya göre bu alan (x) birim kareye eşit:
      3^{2a} = x

  2. Şekil 2’nin Alanı:

    • Şekil 2, bir kenar uzunluğu (27^a) olan kareden bir kenar uzunluğu 3 birim olan küçük bir kare çıkartılarak elde edilmiştir.

    • Öncelikle kendi alanını bulalım:

      \text{Kare Alan Şekil 2} = (27^a)^2 = (3^3)^a = 3^{3a} \times 3^{3a} = 3^{6a}

    • Küçük karenin alanı ise:

      3 \times 3 = 9

    • Şekil 2’nin alanı bu iki değerin farkıdır:

      \text{Alan Şekil 2} = 3^{6a} - 9

  3. Sonucu (x) Cinsinden Yazmak:

    • (3^{2a} = x) olduğuna göre, (3^{6a}) ifadesini (x) cinsinden ifade etmek için şu adımı izleyebiliriz:
      [
      3^{6a} = (3^{2a})^3 = x^3
      ]
    • O halde, Şekil 2’nin alanı:
      \text{Alan Şekil 2} = x^3 - 9

Bu durumda, Şekil 2’nin alanı (x) cinsinden (\boxed{x^3 - 9}) birim kare olarak ifade edilir.