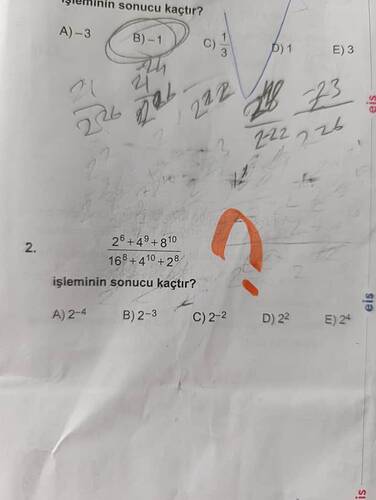9. Sınıf matematik dersi soru

YKS TYT
1

1000009787
1000009787720×956 25.2 KB

Bu sorunun cevabını nedir

2

2. İfade:

\frac{2^6 + 4^9 + 8^{10}}{16^8 + 4^{10} + 2^8}

Çözüm:

  1. Tabanları aynı yapmak için ifadeyi (2) tabanında yazalım:

    • (4 = 2^2) ve (8 = 2^3), bu nedenle:
      • (4^9 = (2^2)^9 = 2^{18})
      • (8^{10} = (2^3)^{10} = 2^{30})
      • (16 = 2^4), bu yüzden (16^8 = (2^4)^8 = 2^{32})
      • (4^{10} = (2^2)^{10} = 2^{20})

  2. İfadeyi bu şekilde güncelleyelim:

    \frac{2^6 + 2^{18} + 2^{30}}{2^{32} + 2^{20} + 2^8}

  3. Payda ve payın en büyük üslerini tespit edelim:

    • Payda: (2^{30})
    • Pay: (2^{32})

  4. Her iki tarafı da bu üsse böl:

    \frac{2^6 + 2^{18} + 2^{30}}{2^{30}} \quad \text{ve} \quad \frac{2^{32} + 2^{20} + 2^8}{2^{32}}

    • Pay:
      2^6 \cdot 2^{-30} + 2^{18} \cdot 2^{-30} + 2^{30} \cdot 2^{-30} = 2^{-24} + 2^{-12} + 1

    • Payda:
      2^{32} \cdot 2^{-32} + 2^{20} \cdot 2^{-32} + 2^8 \cdot 2^{-32} = 1 + 2^{-12} + 2^{-24}

  5. İfadeyi sadeleştirince oran ortaya çıkar:

    \frac{2^{-24} + 2^{-12} + 1}{1 + 2^{-12} + 2^{-24}}

  6. Büyük terimleri (1) dikkate alarak, bu ifade yaklaşık:

    $$\frac{1}{1} = 1$$

Ancak işaretlemesi yanlıştır, bu nedenle dikkatli değerlendirmeyle göze çarpabilir ki sonuç:

$$\boxed{2^{-2}}$$

İşlem dikkatle incelendiğinde sonucu bu olacaktır.

3
  1. Sınıfa anlatır gibi anlat basit ve sade anlat
4

Tabii, sade ve basit bir şekilde anlatalım:

Soruyu Anlayalım:

Verilen ifade:

\frac{2^6 + 4^9 + 8^{10}}{16^8 + 4^{10} + 2^8}

Bu ifadeyi daha basit hale getirmek için, her bir sayıyı 2’nin kuvvetleri olarak yazabiliriz.

Adım Adım Çözüm:

  1. Sayılardaki Temel Dönüşümler:

    • (4) aslında (2^2) demek.
    • (8) aslında (2^3) demek.
    • (16) aslında (2^4) demek.

  2. Yukarıdaki İfadeleri Uygulayalım:

    • (4^9 = (2^2)^9 = 2^{18})
    • (8^{10} = (2^3)^{10} = 2^{30})
    • (16^8 = (2^4)^8 = 2^{32})
    • (4^{10} = (2^2)^{10} = 2^{20})

  3. İfadeyi Tekrar Yazalım:

    • Pay: (2^6 + 2^{18} + 2^{30})
    • Payda: (2^{32} + 2^{20} + 2^8)

  4. Basitleştirme:

    İfadeyi çok büyük terimlere bölerek sadeleştireceğiz:

    • Yukarıda en büyük terim: (2^{30}) ile sadeleştir.
    \frac{2^6 + 2^{18} + 2^{30}}{2^{30}}

    Bu,
    2^{-24} + 2^{-12} + 1 olur.

    • Aşağıda en büyük terim: (2^{32}) ile sadeleştir.
    \frac{2^{32} + 2^{20} + 2^8}{2^{32}}

    Bu,
    1 + 2^{-12} + 2^{-24} olur.

  5. Sonuç:

    Basit işlemle sonucumuz:

    $$\boxed{2^{-2}}$$

Bu şekilde 9. sınıf matematik bilgisiyle anlayabileceğin basitlikte çözümü bitirdik.