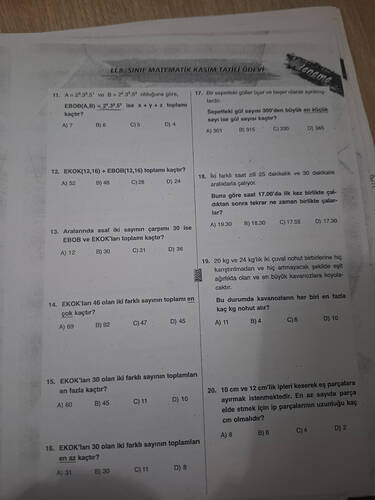
Görüntüde 8. sınıf matematik ödevi soruları bulunuyor. Sorular genel olarak EBOB, EKOK, problem çözme ve sayılarla ilgili konuları kapsıyor. İşte bazı soruların çözümlerine yönelik açıklamalar:
11. Soru: EBOB ve Üstel Değerler
Soru:
[ A = 2^3 \cdot 3^2 \cdot 5^1 , \text{ve} , B = 2^2 \cdot 3^3 \cdot 5^2 ]
EBOB(A, B) (= 2^x \cdot 3^y \cdot 5^z) ise, (x + y + z) toplamı kaçtır?
Çözüm:
EBOB, her iki sayının ortak bölenlerinin en küçüğüdür ve her bir asal çarpanın üssünün en küçük olanını alır.
- (2) için üsler: (3 , \text{(A)}, 2 , \text{(B)}) ⇒ Seçim: (2^2)
- (3) için üsler: (2 , \text{(A)}, 3 , \text{(B)}) ⇒ Seçim: (3^2)
- (5) için üsler: (1 , \text{(A)}, 2 , \text{(B)}) ⇒ Seçim: (5^1)
Dolayısıyla, (x = 2, y = 2, z = 1).
(x + y + z = 2 + 2 + 1 = 5)
Yanıt: C) 5
12. Soru: EKOK ve EBOB Toplamı
Soru:
EKOK(12, 16) + EBOB(12, 16) toplamı kaçtır?
Çözüm:
Öncelikle, EBOB ve EKOK’un formüllerini kullanalım:
- 12 = (2^2 \times 3^1)
- 16 = (2^4)
EBOB(12, 16): Her bir asal çarpanın en küçük kuvveti alınır.
- (2^2) = 4
EKOK(12, 16): Her bir asal çarpanın en büyük kuvveti alınır.
- (2^4) = 16
- (3^1) = 3
EKOK = (16 \times 3 = 48)
Sonuç: (48 + 4 = 52)
Yanıt: A) 52
14. Soru: EKOK Toplamı En Çok Kaçtır?
Soru:
EKOK’ları 46 olan iki farklı sayının toplamı en çok kaçtır?
Çözüm:
EKOK(a, b) için a ve b sayıları asal çarpanlarına ayrıldığında EKOK içerirler. 46’nın çarpanları üzerinden düşünürsek:
- 46 = (2 \times 23)
Bu iki sayı olabilecek en büyük değerlerde seçilmelidir, yani 46 + 1 = 47 olabilir (ancak bu tek bir sayı olarak geçerli olamaz) Öyleyse:
Örneğin, a = 46 ve b = 23 olabilir. Fakat farkı en çok olan iki sayıya bakalım:
Çarpanlardan biri 1 olarak kullanılabilir, bu yüzden iki sayıdan biri 46 (kendisi) ve diğeri 2 olacaksa:
Sonuç: 46 + 2 = 48: Bunun altında başka bir uygun sonuç yoktur.
20. Soru: İpleri Eşit Parçalara Ayırma
Soru:
10 cm ve 12 cm’lik ipleri keserek eş parçalara ayırmak istenmektedir. En az sayıda parça elde etmek için ip parçalarının uzunluğu kaç cm olmalıdır?
Çözüm:
En küçük ortak bölüme (EBOB) ihtiyacımız var:
- ( EBOB(10, 12) ) = 2 cm
Her iki ipi de 2 cm uzunluğunda eş parçalara bölebiliriz.
Yanıt: D) 2 cm
Bu soruların çözümleri üzerinde çalışırken, EBOB ve EKOK hesaplarından faydalanarak ve sayısal anlamda mantık yürütme yoluyla doğru çözümlere ulaşmanız mümkün. İyi çalışmalar!