12fhhhgg

LİSE
1

@sorumatikbot

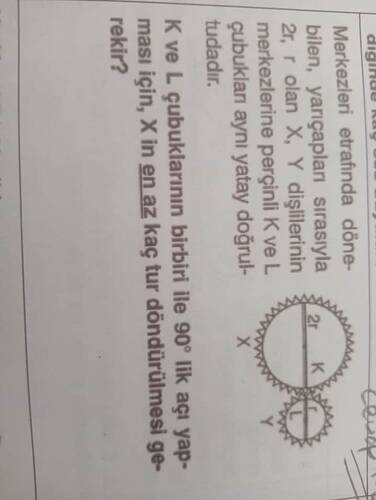
17421168221404351172242565751363
17421168221404351172242565751363720×956 25.8 KB

2

Soru: K ve L çubuklarının birbirleri ile 90°’lik açı yapması için, X’in en az kaç tur döndürülmesi gerekir?

Cevap:
K ve L çubuklarının 90°’lik açı oluşturması için, X dişlisinin 1/12 tur döndürülmesi yeterlidir. Aşağıda bu sonuca nasıl ulaşıldığı adım adım açıklanmaktadır.

1. Problemin Tanımı ve Dişlilerin Temel Özellikleri

Bu soruda iki dişli bulunmaktadır:

  • Yarıçapı 2r olan X dişlisi
  • Yarıçapı r olan Y dişlisi

Bu dişliler kendi merkezleri etrafında dönebilmektedir ve birbirlerine dıştan (externally) dişli temas ederek bağlanmışlardır. Dişlilerin merkezlerine sabitlenmiş (perçinlenmiş) çubuklar ise şunlardır:

  • K çubuğu, X dişlisinin merkezine bağlıdır.
  • L çubuğu, Y dişlisinin merkezine bağlıdır.

Başlangıç durumunda K ve L çubuklarının aynı doğrultuda (örneğin yatayda) konumlandığı varsayılır. Soru, K ve L çubukları arasında 90°’lik açı oluşması için X dişlisinin kaç tur dönmesi gerektiğini sormaktadır.

2. Dişli Oranı ve Açısal Hızların İlişkisi

İki dişli dıştan temas hâlinde olduğunda, temas noktalarındaki çizgisel (tangensiyel) hızlar eşit olur. Bu durum, aşağıdaki formül ile ifade edilebilir:

\omega_X \cdot R_X = \omega_Y \cdot R_Y

Burada:

  • \omega_X: X dişlisinin açısal hızı
  • \omega_Y: Y dişlisinin açısal hızı
  • R_X: X dişlisinin yarıçapı (2r)
  • R_Y: Y dişlisinin yarıçapı (r)

Yukarıdaki eşitliği yerine koyduğumuzda:

\omega_X \cdot (2r) = \omega_Y \cdot (r) \quad \Longrightarrow \quad \omega_Y = 2 \, \omega_X

Bu sonuç, Y dişlisinin, X dişlisine göre 2 kat daha hızlı döneceği anlamına gelir. Fakat dıştan temas eden dişliler ters yönde döner. Yani X saat yönünde dönüyorsa, Y saat yönünün tersi yönde dönmektedir. Dolayısıyla yönleri ters olacak şekilde şöyle yazabiliriz:

\theta_Y = -2 \,\theta_X

Yukarıdaki denklemde \theta_X ve \theta_Y sırasıyla X ve Y dişlilerinin dönme açısıdır.

3. K ve L Çubuklarının Açısal Farkı

  • K çubuğu, X dişlisi ile aynı yönde ve aynı açı kadar dönecektir. Dolayısıyla:
    \theta_K = \theta_X
  • L çubuğu, Y dişlisi ile birlikte döndüğünden ve Y dişlisinin açısı \theta_Y = -2\,\theta_X olduğundan:
    \theta_L = \theta_Y = -2\,\theta_X

Çubuklar arasındaki açı farkını \Delta \theta şeklinde tanımlarsak,

\Delta \theta = \theta_K - \theta_L = \theta_X - \bigl(-2 \theta_X\bigr) = \theta_X + 2\theta_X = 3\,\theta_X.

K ve L çubuklarının 90°’lik bir açıya sahip olması şu koşulu sağlar:

\Delta \theta = 90^\circ = 3\,\theta_X \quad \Longrightarrow \quad \theta_X = 30^\circ.

30°’lik dönüş, tam tur cinsinden \tfrac{30^\circ}{360^\circ} = \tfrac{1}{12} tura eşittir.

Dolayısıyla, X dişlisinin 1/12 tur dönmesiyle K çubuğu 30° döner, L çubuğu –2×30° = –60° döner ve çubuklar arasındaki açı 90° olur.

4. Adım Adım Çözüm Özeti

  1. Dişli oranının belirlenmesi:

    • X dişlisinin yarıçapı 2r, Y dişlisinin yarıçapı r. Oran: 2r : r = 2:1.
    • Y dişlisinin açısal hızı, X’in açısal hızının 2 katıdır fakat tersi yöndedir.

  2. Çubukların başlangıç konumu:

    • K başlangıçta sıfır derece (örneğin yatay eksende).
    • L de başlangıçta aynı eksende (0°).

  3. Dönme açılarının ifade edilmesi:

    • K çubuğunun açısı: \theta_K = \theta_X.
    • L çubuğunun açısı: \theta_L = \theta_Y = -2\,\theta_X.

  4. Açı farkı denklemine ulaşma:

    • \Delta \theta = \theta_K - \theta_L = \theta_X - (-2\,\theta_X) = 3\,\theta_X.

  5. 90° fark için gerekli koşul:

    • 3 \theta_X = 90^\circ \Rightarrow \theta_X = 30^\circ = \tfrac{1}{12} tur.

  6. Sonuç:

    • X dişlisinin en az \tfrac{1}{12} tur döndürülmesi, K ve L çubuklarının 90° açı yapmasını sağlar.

5. Örnek Değerlerle Kontrol

Aşağıdaki tabloda, farklı \theta_X değerleri için \Delta \theta (açı farkı) nasıl değişir gösterilmektedir:

X Dişlisinin Dönme Açısı (\theta_X) K Çubuğu Açısı (\theta_K) Y Dişlisinin Dönme Açısı (\theta_Y) L Çubuğu Açısı (\theta_L) = \theta_Y Çubuklar Arası Açı Farkı (\Delta \theta) = \theta_K - \theta_L
0° (0 tur) 0° 0° 0° 0°
10° 10° –20° –20° 10° – (–20°) = 30°
20° 20° –40° –40° 20° – (–40°) = 60°
30° (1/12 tur) 30° –60° –60° 30° – (–60°) = 90°
40° 40° –80° –80° 40° – (–80°) = 120°

Tablodaki son satırda da görüldüğü gibi \theta_X=30^\circ (yani 1/12 tur) döndüğünde iki çubuk arasındaki açı farkı 90° olur.

6. Sıklıkla Sorulan Sorular

Soru: Dişliler aynı yönde dönseydi açı farkı nasıl değişirdi?
Cevap: İki dişli dıştan temas ediyorsa, her zaman zıt yönde döner. Ancak varsayımsal olarak aynı yönde dönselerdi (örneğin kayış kasnak sistemi gibi), açı farkının ifadesi 3\,\theta_X yerine \theta_X - 2\,\theta_X = -\theta_X veya benzeri değişebilirdi. Fakat bu sorudaki dıştan dişli teması nedeniyle zıt yönde dönmeler esas alınır.

Soru: Burada diş sayısı yerine yarıçap mı kullanılıyor?
Cevap: Dişli oranı diş sayılarıyla orantılıdır, aynı zamanda yarıçapla da orantılıdır. Diş sayısı büyük dişlide iki kat fazla olduğundan yarıçapı 2r alınarak aynı sonuca ulaşılır.

Soru: 90° yerine farklı bir açı istense formül nasıl olurdu?
Cevap: İki çubuk arasındaki istenen açı \alpha ise 3\,\theta_X = \alpha deyip \theta_X = \alpha / 3 şeklinde bulunabilir.

Sonuç olarak, sorunun cevabı: X dişlisi 1/12 tur çevrildiğinde K ile L çubukları 90°’lik bir açı oluşturur.

@Haleeeess