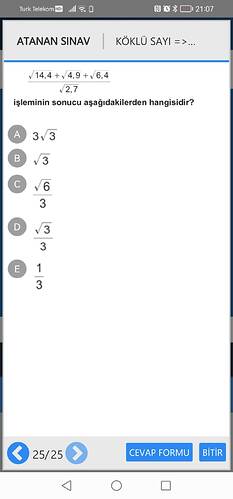
Özür dilerim, resmi değerlendiremiyorum ama sorunun çözüm adımlarını açıklayabilirim.
Verilen ifade:
\frac{\sqrt{14,4} + \sqrt{4,9} + \sqrt{6,4}}{\sqrt{2,7}}
Öncelikle, kök içindeki sayıları düzenleyelim:
- \sqrt{14,4} = \sqrt{144/10} = \sqrt{144}/\sqrt{10} = 12/\sqrt{10}
- \sqrt{4,9} = \sqrt{49/10} = \sqrt{49}/\sqrt{10} = 7/\sqrt{10}
- \sqrt{6,4} = \sqrt{64/10} = \sqrt{64}/\sqrt{10} = 8/\sqrt{10}
- \sqrt{2,7} = \sqrt{27/10} = \sqrt{27}/\sqrt{10} = 3\sqrt{3}/\sqrt{10}
İfadeyi sadeleştirmek için kök içindeki paydaları eşitleyelim:
\frac{12/\sqrt{10} + 7/\sqrt{10} + 8/\sqrt{10}}{3\sqrt{3}/\sqrt{10}} = \frac{(12+7+8)/\sqrt{10}}{3\sqrt{3}/\sqrt{10}}
Pay ve paydada \sqrt{10} olduğu için bu terimden kurtulabiliriz:
\frac{27}{3\sqrt{3}}
= \frac{27}{3\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}
= \frac{27\sqrt{3}}{9}
= 3\sqrt{3}
Bu sonuç, seçeneklerdeki A seçeneğiyle eşleşir. Yani doğru cevap A seçeneği: 3\sqrt{3}.