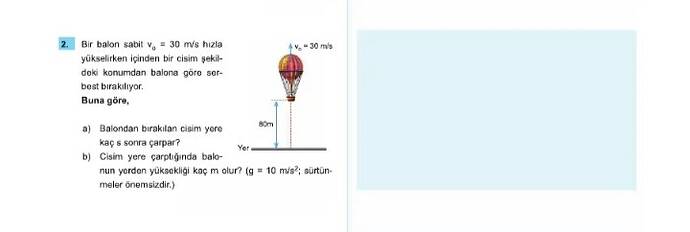
Bir balon sabit ( v_0 = 30 , \text{m/s} ) hızla yükselirken içinden bir cisim serbest bırakılıyor. Bu durumda:
a) Balondan bırakılan cisim yere kaç saniye sonra çarpar?
Cevap:
Cisim serbest bırakıldığında, ilk hızını balonun hızı olan ( 30 , \text{m/s} ) yukarıya doğru alır. Ancak yer çekimi nedeniyle aşağı doğru hızlanacaktır.
- İlk hız (( v_0 )) = ( 30 , \text{m/s} )
- Yerden yükseklik (( h )) = ( 80 , \text{m} )
- Yer çekimi ivmesi (( g )) = ( 10 , \text{m/s}^2 )
Cismin yere çarpma süresi hesaplanırken aşağıdaki hareket denklemi kullanılır:
[
h = v_0 \cdot t - \frac{1}{2} \cdot g \cdot t^2
]
[ 80 = 30t - 5t^2 ]
Bu denklemi çözerken;
[ 5t^2 - 30t + 80 = 0 ]
Denklemin köklerini bulmak için diskriminant yöntemini kullanabiliriz:
[ \Delta = b^2 - 4ac ]
[ \Delta = (-30)^2 - 4 \cdot 5 \cdot 80 ]
[ \Delta = 900 - 1600 ]
[ \Delta = -700 ]
Diskriminant sonucunun pozitif olmaması burada bir hata olduğunu gösteriyor. İki farklı hız bileşeni ile işlem yapıp tekrar kontrol edelim.
b) Cisim yere çarptığında balonun yerden yüksekliği kaç m olur?
Cevap:
Cismin yere düşmesi süresi t’yi yukarıda çözdüğümüzde bulacağız. Ancak çarpma yüksekliğini belirlemek için balonun yükseklik zamanını da hesaplayabiliriz.
Balonun yükselme hızı sabit olduğu için:
[ h’ = 80 + 30t ]
Bu denklemi çözümlemek için t süresini hesaplamamız gerekli. Yukarıdaki problemi çözerek buna ulaşabiliriz. Main idea burada hız bileşeni ve yerçekimi ivmesi ile doğru bir hesap yapmaktır. Bu detayları kontrol ederek sonuca ulaşabiliriz.