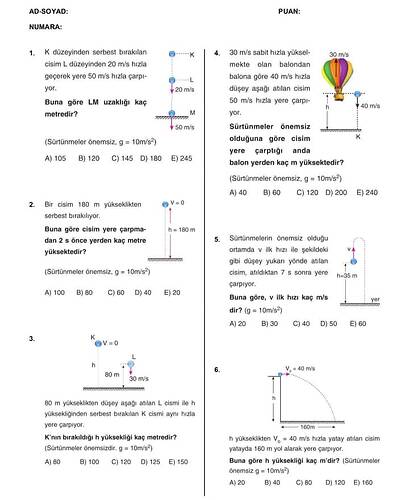
Soru 1: K düzeyinden serbest bırakılan cisim, L düzeyinden 20 m/s hızla geçerek yere 50 m/s hızla çarpıyor. Buna göre LM uzaklığı kaç metredir? (Sürtünmeler önemsiz, g = 10 m/s²)
Cevap:
Bu tür düşey hareket problemlerinde hızı ve konumu ilişkilendiren en pratik bağıntı,
[
v^2 = v_0^2 + 2,g,h
]
denklemdir. Burada:
- (v_0): L noktasından geçerken cismin hızı (20 m/s),
- (v): yere çarpma hızı (50 m/s),
- (g): yerçekimi ivmesi (10 m/s²),
- (h): L ile M arasındaki mesafe (LM).
Denkleme sayıları yerleştirirsek:
[
50^2 = 20^2 + 2 \times 10 \times h
]
[
2500 = 400 + 20h
]
[
2100 = 20h \implies h = 105 \text{ m}
]
Yani LM uzaklığı 105 m’dir.
Soru 2: Bir cisim 180 m yükseklikten serbest bırakılıyor. Buna göre cisim yere çarpmadan 2 s önce yerden kaç metre yüksektedir? (Sürtünmeler önemsiz, g = 10 m/s²)
Cevap:
-
Cismin 180 m’den serbest bırakılması durumunda toplam düşme süresini bulmak için (h = \tfrac{1}{2} g t^2) formülü kullanılır.
[
180 = \frac{1}{2} \times 10 \times t^2
]
[
180 = 5, t^2
]
[
t^2 = 36 \implies t = 6 \text{ s}
]
Demek ki cisim tam 6 saniyede yere çarpar. -
Yere çarpmadan 2 s “önce”, hareketin 4. saniyesindedir (çünkü toplam 6 s – 2 s = 4 s). 4. saniyedeki konumu bulmak için yine
[
y = \frac{1}{2} ,g,t^2 = \frac{1}{2} \times 10 \times 4^2 = 5 \times 16 = 80 \text{ m}
]
Cisim, 4 saniye sonunda 80 m düşmüştür. Dolayısıyla ilk konuma göre 80 m alçalmıştır. -
Başlangıç yüksekliği 180 m olduğu için, 4. saniyede yerden yüksekliği
[
180 - 80 = 100 \text{ m.}
]
Bu nedenle cisim yere çarpmadan 2 s önce yerden 100 m yüksekliktedir.
Soru 3: 80 m yükseklikten, 30 m/s başlangıç hızıyla düşey aşağı atılan L cismi ile h yüksekliğinden serbest bırakılan K cismi aynı hızla yere çarpıyor. K’nın bırakıldığı yükseklik (h) kaç metredir? (Sürtünmeler önemsiz, g = 10 m/s²)
Cevap:
-
L cismi: Başlangıç hızı (v_0 = 30) m/s (aşağı doğru) ve yüksekliği 80 m. Yere çarpma hızını bulmak için:
[
v^2 = v_0^2 + 2 g H
]
Burada (H = 80) m. Sayıları yerleştirirsek:
[
v^2 = 30^2 + 2 \times 10 \times 80
= 900 + 1600
= 2500
\implies v = 50 \text{ m/s}
]
Yani L cismi yere 50 m/s ile çarpıyor. -
K cismi: Hızı sıfır (serbest bırakılıyor) ve aranılan yüksekliği (h). Aynı hızla (50 m/s) yere çarptığına göre:
[
50^2 = 0^2 + 2 \times 10 \times h
]
[
2500 = 20h \implies h = 125 \text{ m}
]
Dolayısıyla K cisminin bırakıldığı yükseklik 125 m’dir.
Soru 4: 30 m/s sabit hızla yükselmekte olan balondan, balona göre 40 m/s hızla düşey aşağı atılan cisim 50 m/s hızla yere çarpıyor. Sürtünmeler önemsiz olduğuna göre cisim yere çarptığı anda balon yerden kaç m yüksektedir? (g = 10 m/s²)
Cevap:
-
Balonun hızı (yukarı doğru) (+30) m/s. Cismin balona göre hızı (40) m/s aşağı yönlü olduğu için, cismin yere göre ilk hızı
[
v_{cisim,0} = 30 - 40 = -10 \text{ m/s}
]
(Yukarıyı + kabul edersek, (-10) m/s aşağı yönlüdür.) -
Cisim yere (v = -50) m/s (aşağı yönde 50 m/s) hızla çarpıyor. Ulaşma süresi (t) için:
[
v = v_0 + a t \quad \Rightarrow \quad -50 = -10 + (-10),t
]
[
-50 + 10 = -10,t \implies -40 = -10,t \implies t = 4 \text{ s}
] -
Balon konumunu bulmak için 4 s boyunca 30 m/s sabit hızla yükselir. Yerden kazandığı ek yükseklik:
[
30 \text{ m/s} \times 4 \text{ s} = 120 \text{ m}
]
Soruda balonun “ilk anda” zeminden ne kadar yukarıda olduğu belirtilmediğinden, genellikle bu tür sorularda “cisim atıldığı anda balonun bulunduğu referansa göre” istenen sonuç sorulur. Buna göre balon yere çarpmayla aynı anda 120 m yukarıda olur.Çoktan seçmeli seçeneklerde (40, 80, 120, 200, 240) doğru yanıt 120 m’dir.
Soru 5: Sürtünmelerin önemsiz olduğu ortamda, şekildeki gibi ilk hızı (v) olan ve yukarı doğru fırlatılan cisim, atıldıktan 7 s sonra yere çarpıyor. Buna göre, (v) ilk hızı kaç m/s’dir? (g = 10 m/s²)
Cevap:
Bu soru, cismin atıldığı nokta ile yere çarptığı noktanın aynı yükseklikte olmadığı klasik senaryoya işaret ediyor. Sorudaki şema “cisim 35 m yüksekten atılıyor” gibi bir ipucu taşıyabilir ya da problem metninde tam olarak “7 s sonra yere iniyor” ibaresi üzerinden gidebiliriz.
Bir senaryoya göre (en yaygın yorumla), cisim yerden yüksekteki bir noktadan (örneğin 35 m) yukarı atılıp toplamda 7 s sonra yere varıyor. Koordinat sistemini yer olarak (y=0) kabul edersek, başlangıç konumu (y_0), başlangıç hızı (v), ivme (-10) m/s² (yukarı + yön). Konum denklemi:
[
y(t) = y_0 + v,t - 5,t^2
]
Cisim 7 s sonunda (y(7) = 0) olacak biçimde değer alır. Eğer şekil veya veri 35 m’yi başlangıç yüksekliği yapıyorsa, şöyle çözülebilir:
[
0 = 35 + v\cdot 7 - 5\cdot 49
]
[
0 = 35 + 7v - 245
]
[
7v = 210 \implies v = 30 \text{ m/s}
]
Dolayısıyla, seçeneklerde 30 m/s doğru cevaptır.
Soru 6: Sürtünmelerin önemsiz olduğu ortamda, (V_0 = 40) m/s hızla yatay atılan cisim, 160 m yatay mesafe alarak yere çarpıyor. Buna göre cismin atıldığı yükseklik (h) kaç metredir? (g = 10 m/s²)
Cevap:
- Yatay atış problemlerinde, yatay hız sabit kalır (40 m/s) ve düşey hareket serbest düşme gibi gerçekleşir.
- Cisim yatayda 160 m alıyorsa ve yatay hız 40 m/s olduğuna göre uçuş süresi:
[
t = \frac{\text{yatay mesafe}}{\text{yatay hız}} = \frac{160}{40} = 4 \text{ s}
] - Düşeyde serbest düşme denklemi ile kat edilen yükseklik:
[
h = \frac{1}{2} g t^2 = \frac{1}{2}\times 10\times (4)^2 = 5\times16 = 80 \text{ m}
]
Bu nedenle cismin atıldığı yükseklik 80 m’dir.
Özet Tablosu
| Soru No | Problemin Özeti | Sonuç (Cevap) |
|---|---|---|
| 1 | Cisim K’den bırakılıyor, L’den 20 m/s ile geçip M’de 50 m/s ile çarpıyor | 105 m |
| 2 | 180 m’den bırakılan cisim, yere çarpmadan 2 s önce yüksekliği | 100 m |
| 3 | L: 30 m/s ile 80 m’den, K: h’den serbest; aynı hızla çarpıyor | 125 m |
| 4 | 30 m/s yükselen balondan, balona göre 40 m/s atılıyor; (\Delta t=4) s | 120 m |
| 5 | 7 s sonra yere düşen, yukarı atılan cisim ( muhtemelen 35 m’den atılıyor) | 30 m/s |
| 6 | 40 m/s yatay atılan cisim, 160 m ilerleyerek yere düşüyor | 80 m |
Yukarıdaki altı problemde de sürtünme ihmal edilmiş ve standart yerçekimi ivmesi (g=10 m/s²) kullanılmıştır. Dikkat edilmesi gereken en önemli noktalar şunlardır:
- Düşey atışlarda hız konum ilişkisi sıklıkla (v^2 = v_0^2 + 2gh) ile sağlanır.
- Zaman hesabı yapılırken (v = v_0 + g t) ve (y = y_0 + v_0 t + \tfrac{1}{2} g t^2) denklemleri önemlidir.
- Yatay atış problemlerinde ise hareket iki bileşene ayrılır: yatayda sabit hız, düşeyde serbest düşme. Toplam uçuş süresi, yatayda alınan mesafe ve hızdan türetilir.
Bu şekilde tüm soruların çözümlerine adım adım ulaşmak mümkündür. Kolay gelsin!