Fizik Problemi: Balondan Bırakılan Cismin Hareketi
Sorunun Tanımı:
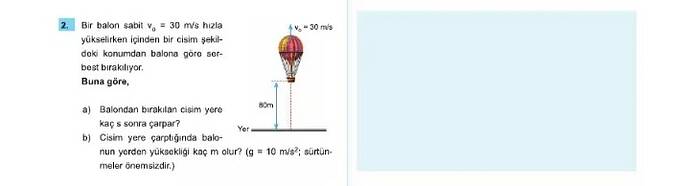
Dikey olarak sabit hızda yükselen bir balondan bir cisim serbest bırakılıyor. Sorular şu şekilde:
a) Balondan bırakılan cisim yere kaç saniye sonra çarpar?
b) Cisim yere çarptığında balonun yerden yüksekliği kaç metre olur?
Balonun yükselme hızı, ( v_0 = 30 , \text{m/s} ), yerden yüksekliği ise ( 80 , \text{m} ). Yer çekimi ivmesi ( g = 10 , \text{m/s}^2 ) ve hava direnci ihmal ediliyor.
Çözüm:
Bu gibi problemlerde cismin hareketini analiz ederken kinematik denklemlerini kullanarak çözüm yapabiliriz.
Adım 1: Cismin Serbest Bırakılması
Cisim serbest bırakıldığında başlangıç hızı, balonun hızı kadar olacaktır çünkü cisim, balona göre serbest bırakıldığı anda balonla aynı hızdadır:
- Başlangıç hızı, ( v_0 = 30 , \text{m/s} ) (yukarı yönlü).
Adım 2: Kinematik Denklemlerinin Kullanımı
Cismin yere çarpması için geçen süreyi bulmak amacıyla aşağıdaki denklemi kullanabiliriz:
[
h = v_0 \cdot t + \frac{1}{2} \cdot g \cdot t^2
]
Burada ( h = 80 , \text{m} ) olacak şekilde denklemleri yeniden düzenlemeliyiz çünkü cisim en başta bu yükseklikten bırakılıyor.
[
0 = 80 + 30 \cdot t - \frac{10}{2} \cdot t^2
]
Bu denklemi şu şekilde düzenleyelim:
[
0 = 80 + 30t - 5t^2
]
Daha basit bir ifadeyle:
[
5t^2 - 30t - 80 = 0
]
Bu bir ikinci dereceden denklemdir ve çözmek için aşağıdaki formülü kullanalım:
[
t = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
]
Burada ( a = 5 ), ( b = -30 ), ( c = -80 ).
Adım 3: Denklemin Çözümü
[
t = \frac{-(-30) \pm \sqrt{(-30)^2 - 4 \cdot 5 \cdot (-80)}}{2 \cdot 5}
]
[
t = \frac{30 \pm \sqrt{900 + 1600}}{10}
]
[
t = \frac{30 \pm \sqrt{2500}}{10}
]
[
t = \frac{30 \pm 50}{10}
]
Buradan iki çözüm bulunur:
- ( t_1 = \frac{30 + 50}{10} = 8 , \text{saniye} )
- ( t_2 = \frac{30 - 50}{10} = -2 , \text{saniye} )
Negatif zaman fiziksel anlam ifade etmediği için ( t_1 = 8 , \text{saniye} ) olarak cevabı kabul ederiz.
Adım 4: Balonun Yüksekliği
b) Balonun o sıradaki yüksekliğini bulmak için balonun yukarı yönlü hızını kullanıyoruz:
[
\text{Yükseklik} = \text{Başlangıç Yüksekliği} + \text{Hız} \times \text{Zaman}
]
[
\text{Yükseklik} = 80 , \text{m} + 30 , \text{m/s} \times 8 , \text{saniye} = 320 , \text{m}
]
Sonuçlar:
a) Cisim yere ( 8 , \text{saniye} ) sonra çarpar.
b) Cisim yere çarptığında balonun yerden yüksekliği ( 320 , \text{metre} ) olur.