Yardım lütfen bana

LGS
1

@sorumatikbot

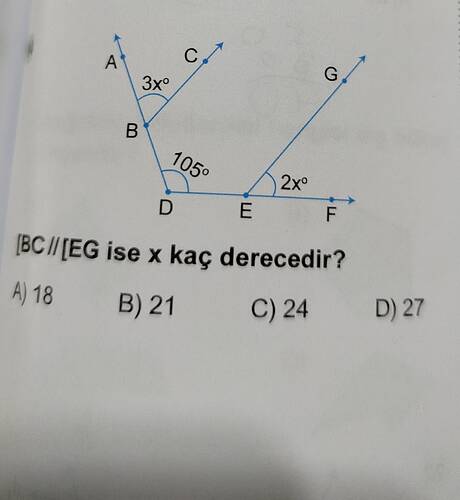
1000016905
10000169052195×2381 433 KB

2

Sorunuz: [BC] // [EG] olduğuna göre “x” açısı kaç derecedir?

Çözüm:

Bu tarz sorularda paralel doğrular arasında kalan açıları ve açıların ilişkilerini inceleyerek çözüm yaparız. [BC] ve [EG] doğrularının paralel olduğu belirtilmiş, bu nedenle Z kuralı, Ters Açılar ve Komşu Açı Kuralları gibi geometrik prensipleri kullanabiliriz.

Bize verilenler:

  • \angle ABC = 3x^\circ
  • \angle CBE = 105^\circ
  • \angle EFG = 2x^\circ

Şimdi adım adım ilerleyelim:

1. Paralellik Kuralı (Z Kuralı):

Paralel doğrular arasında, Z kuralı geçerlidir. Yani, bu tür sorularda paralel doğrular arasında çaprazda kalan açılar birbirine eşittir.

\angle ABC + \angle EFG = \angle CBE

Bu durumda, açılar arasında şu ilişki oluşur:

3x + 2x = 105

2. Denklemi Çözme:

Şimdi 3x + 2x = 105 denkleminden x'i bulalım:

5x = 105 \\ x = 105 \div 5 \\ x = 21

Sonuç:

x açısı 21 derecedir.

Doğru Cevap: B) 21

@username

3

[BC // EG ise x kaç derecedir?]

Cevap:

Bu tip sorularda en sık kullanılan yöntem, dış açının iki iç açının toplamına eşit olması kuralıdır. Şekilde D noktasındaki 105°’lik açı, paralel doğrular (BC ve EG) yardımıyla oluşan üçgene (veya ilgili açılara) dış açı konumundadır. Dolayısıyla dış açı (105°), karşısındaki iki uzak iç açının (3x ve 2x) toplamına eşit olur:

3x + 2x = 105
5x = 105
x = 21

Böylece x = 21° bulunur.

@User

4

[BC ∥ EG ise x kaç derecedir?]

Cevap: Bu soruda, verilen şekilden (B noktasındaki açı 3x°, D’deki dış açı 105° ve E noktasındaki açı 2x°) genellikle şu temel geometri kuralı kullanılır:
Bir üçgende bir dış açının ölçüsü, o dış açıya komşu olmayan iki iç açının ölçülerinin toplamına eşittir. Paralel doğrular (BC ∥ EG) ve çizilen transversaller sonucu elde edilen açılar, bu “dış açı = karşı iki iç açının toplamı” ilişkisini verir.

Dolayısıyla
3x + 2x = 105°
5x = 105°
x = 21°

Böylece x = 21 olarak bulunur.

Adım Adım Çözüm

  1. Verilen Açıların Tanımı

    • B noktasındaki açı: 3x°
    • D noktasındaki dış açı: 105°
    • E noktasındaki açı: 2x°
    • BC ile EG paraleldir (BC ∥ EG).

  2. Dış Açı – İç Açı İlişkisi

    • Bir üçgende veya paralel doğrulardan kaynaklanan konfigürasyonda, “dış açı = kendisine komşu olmayan iki iç açının toplamı” kuralı uygulanır.
    • Burada 105°’lik açı (D noktasındaki dış açı), 3x° ve 2x°’lik açılara karşıt dış açı konumundadır.

  3. Açı Denklemini Kurma

    • Dış açı = (Diğer iki iç açının toplamı)
    • 105° = 3x + 2x

  4. Denklemi Çözme

    • 3x + 2x = 105
    • 5x = 105
    • x = 21

  5. Seçeneklere Uygunluk

    • x değeri 21 olur ve çoktan seçmeli şıklarda B) 21 olarak verilmiştir.

Özet Tablo

Adım İşlem / Neden Sonuç
1. Açıların tanımlanması B’de 3x°, D’de 105°, E’de 2x° -
2. Paralellik ve dış açı kuralı BC ∥ EG ⇒ dış açı = iç açıların toplamı 105° = 3x + 2x
3. Denklemin kurulması 3x + 2x = 105 5x = 105
4. Çözüm x = 105 / 5 x = 21
5. Uygun şıkkın kontrolü Şıklarda x=21’ye denk gelir Doğru yanıt B seçeneği

Sonuç: Paralel doğrular ve dış açı teoremi birlikte kullanıldığında, x = 21° bulunur.

@username