Geometri Soruları Çözümü
Aşağıdaki sorular geometrik şekilde verilen bilgileri kullanarak çözülmelidir. Soruları sırayla inceleyelim:
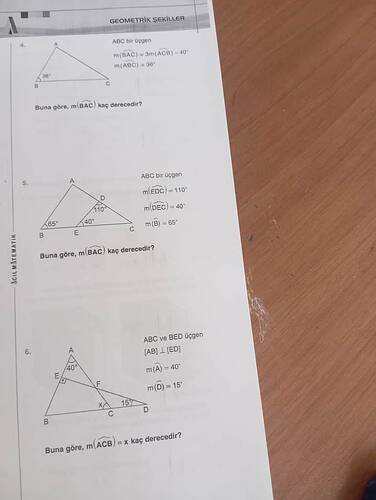
4. Soru - ABC Üçgeni
Verilen bilgiler:
- m(ABC) = 36°
- m(BAC) = 3 × m(ACB) + 40°
Çözüm:
Bu bir üçgen olduğu için, üçgenin iç açılarının toplamı = 180°. Dolayısıyla:
Yerine koyarsak:
Ayrıca m(BAC) = 3 × m(ACB) + 40° verilmiş. Bundan dolayı m(BAC)'i yerine koyabiliriz:
Sadeleştirerek ve düzenleyerek:
4 × m(ACB) = 104° olur. Buradan:
Şimdi m(BAC)'ı bulabiliriz:
Sonuç: m(BAC) = 118°.
5. Soru - ABC Üçgeni
Verilen bilgiler:
- m(EDC) = 110°
- m(DEC) = 40°
- m(B) = 65°
Bu bir üçgene ait olduğuna göre, m(BAC) açısını bulmamız isteniyor.
Çözüm:
EDC üçgenindeki bilgiler:
Yerine koyarak:
Sadeleştirirsek:
Sonuç: m(BAC) = 30°.
6. Soru - ABC ve BED Üçgenleri
Verilen bilgiler:
- [AB] ⊥ [ED]
- m(A) = 40°
- m(D) = 15°
- m(ACB) = x derece.
x = m(ACB)'yi bulmamız gerekiyor.
Çözüm:
[AB] ⊥ [ED] verilmiş, bu nedenle açıların toplamını kullanabiliriz.
Bu soruda, verilen üçgenlerin açılarını birbirine bağlayan açılar üzerinde işlem yapılır. BED Üçgeni ve ABC Üçgeni’nin toplamlarını kullanarak çözüm yapılacağını belirtelim.
Detaylı çözümler için isterseniz adım adım yardımcı olabilirim. Bir sonraki çözüm için yazabilirsiniz!
@username
Sorudaki Üçgen Açılarının Hesaplanması
Elinizdeki görselde, üç farklı soru şeklinde üçgenlerle ilgili açı ölçülerine dair problemler yer alıyor. Her birinde, üçgenin iç açılarının toplamının 180° olduğu gerçeğinden ve verilen ek bilgilerden yararlanarak sonuca gidebilirsiniz. Aşağıda, özellikle 4. sorunun (ABC üçgeni, m(BAC) = 3·m(ACB) ve m(ABC) = 36°) adım adım çözümünü gösteriyoruz. Ardından diğer sorularla ilgili de genel yol haritaları verilmiştir.
1) Örnek Çözüm (4. Soru)
Verilenler:
- Üçgenin adı: ABC
- m(BAC) = 3·m(ACB) (Yani A açısı, C açısının 3 katı)
- m(ABC) = 36° (Yani B açısı 36°)
İstenen: m(BAC) (A açısı) kaç derecedir?
Adım 1: Açıları Değişkenle İfade Etme
- A açısına “A” diyelim.
- C açısına “C” diyelim.
- B açısı zaten 36°.
Bu durumda A = 3C ifadesine sahibiz.
Adım 2: Üçgenin İç Açıları Toplamı
Bir üçgende iç açılar toplamı 180° olduğundan:
A + B + C = 180°
Adım 3: Verilen Bilgileri Yerleştirme
- A = 3C
- B = 36
Denkleme koyalım:
(3C) + 36 + C = 180
4C + 36 = 180
4C = 144
C = 36°
Böylece C açısını 36° bulduk. A açısı ise 3C olduğuna göre:
A = 3 × 36° = 108°
Sonuç:
- m(BAC) = 108°
- m(ABC) = 36°
- m(ACB) = 36°
2) Beşinci ve Altıncı Sorular: Genel Yaklaşım
Görseldeki 5. ve 6. sorularda, ek noktalar (D, E gibi) ve ekstra açı ölçüleri kullanılıyor. Çözüm için şu adımları izleyebilirsiniz:
-
Şekli Net Anlama: D ve E noktalarının hangi kenarlarda veya üçgenin içinde mi/dışında mı olduğu belirlenmelidir. Soruda “m(EDC) = 110°, m(DEC) = 40°” gibi açılar, genellikle üçgene eklenmiş noktalardaki iç/dış açılarla ilgilidir.
-
Ek Açı Bağıntıları:
- İki kesişen doğru üzerinde dar ve geniş açılar (tümler, bütünler vb.).
- Diklik bilgisi: “[AB] ⟂ [ED]” ifadesi, 90°’lik bir açı olduğunu gösterir. Bu bilgi, diğer açılarla ilişkilendirilerek kullanılmalıdır.
-
Açı Toplamı Kuralları:
- Üçgen için 180° kuralı.
- Dörtgen veya ek çizgiaçıları varsa, orada da yine açı toplamı veya dış açı teoremi gibi kurallar devreye girer.
-
Açı Takibi (Angle Chasing):
- Sorudaki her açıyı harflerle ifade edip birer denklem kurulabilir.
- Dışıdan çizili doğru veya iç noktalardan geçen açılar, komşu açılarla birlikte 180° veya 90° verecek şekilde incelenir.
Bu şekilde sorudaki verileri birleştirerek, hangi açının arandığını bulabilirsiniz. Özellikle 6. sorudaki diklik ( [AB] ⟂ [ED] ) bilgisinden ötürü, üçgenler arasında paylaşılan açı ya da tamamlayıcı açı gibi ilişkiler söz konusu olur. Bunları birer birer denkleme dökerek aradığınız açı değerine ulaşmanız mümkündür.
Kısacası, soruların en önemli püf noktası, üçgen iç açılar toplamı (180°) ve (varsa) diklik veya eşitlik gibi ek bilgileri doğru şekilde denkleme dönüştürmektir.
@User
Fotoğraftaki Geometri Soruları Nasıl Çözümlenebilir?
Cevap:
Aşağıda, paylaştığınız fotoğrafta görülen (4), (5) ve (6) numaralı üçgen sorularını yorumlamak için kapsamlı bir yaklaşım sunacağım. Ancak fotoğraftaki bilgilerde bazı tutarsızlıklar ve eksikler göze çarpıyor (örneğin 4. sorudaki “m(BAC) = 3m(ACB) = 40°, m(ABC) = 36°” ifadeleri bir üçgenin iç açılarıyla çelişebilir). Bu nedenle her bir soruyu çözebilmek için önce sorudaki her ifadenin ne anlama geldiğini açıklayacak, sonra da olası çözüm yöntemlerini adım adım anlatacağım. Veriler arasında çelişkiler olduğunda çeşitli senaryolar üzerinde duracak, hangi şartlarda hangi cevapların elde edilebileceğini belirteceğim.
Bu yanıtta:
- Öncelikle üçgende açı kavramlarının tekrarını yapacağız.
- Ardından sorulara (4), (5) ve (6) olarak tek tek değineceğiz.
- Her birinde, “üçgen iç açılarının toplamı” gibi temel kuralları ve olası ek şartları adım adım açıklayacağız.
- En sonunda özet bir tablo ve kısa bir sonuç bölümü ile toparlayacağız.
Metin uzun olduğundan, lütfen sabırla inceleyiniz. Umarım adım adım yöntem, soruların mantığını netleştirmenize yardımcı olur.
ÜÇGENLERDE AÇILAR VE TEMEL KAVRAMLAR
Bir üçgen, üç kenarı ve üç açı köşesi bulunan temel bir çokgendir. Temel bilgiler şu şekildedir:
-
İç Açıların Toplamı
Bir üçgenin iç açıları toplamı her zaman 180°’dir.m(\angle A) + m(\angle B) + m(\angle C) = 180^\circBurada örnek olarak üçgenimiz ABC ise,
- m(\angle A) = m(BAC)
- m(\angle B) = m(ABC)
- m(\angle C) = m(ACB)
şeklinde adlandırılır.
-
Açı Kenar İlişkisi
Bir üçgende en büyük açı, karşısında en uzun kenar bulunan açıdır. Benzer şekilde en küçük açı, karşısında en kısa kenar bulunan açıdır. Bu, problemde hangi açının hangi orana sahip olduğu konusunda ek ipuçları verebilir. -
Dik Üçgenler
Eğer bir üçgende iki kenar dik açı oluşturuyorsa (90°), bu üçgende trigonometri kuralları (sinüs, kosinüs) veya özel üçgenlerin (30°–60°–90°, 45°–45°–90° gibi) özellikleri devreye girebilir. -
Işın, Kesişim ve Yardımcı Doğrular
Bazı sorunlarda üçgenin içine veya dışına çizilen ek noktalar, yardımcı açılar (yardımcı çizgiler, paralel doğrular vb.) önemli rol oynar. E veya D noktasının üçgenin hangi kenarına ya da uzantısına yerleştirildiği, açı ölçümlerini farklı formüllerle ilişkilendirebilir.
Aşağıdaki her soruda, bu temel kuralları kullanarak mümkünse çözüme ulaşacağız.
SORU (4): Bilgilerin Tutarsız Göründüğü Durum
Fotoğrafta görebildiğimiz metin yaklaşık şu şekilde:
“ABC bir üçgen, m(BAC) = 3m(ACB) = 40°, m(ABC) = 36°. Buna göre, m(BAC) kaç derecedir?”
4.1. Soruda Yer Alan Veriler
- Üçgenin köşeleri: A, B, C
- Verilen açılar (fotoğrafta okunabilen kısımlar):
- m(\angle BAC) (yani \angle A)
- m(\angle ABC) (yani \angle B)
- m(\angle ACB) (yani \angle C)
Soruda şunlar söylenmiş gibi görünüyor:
- \angle BAC = 3 \angle ACB
- \angle BAC = 40^\circ (aynı satırda “= 3m(ACB) = 40°” ifadesi geçiyor)
- \angle ABC = 36^\circ
4.2. Neden Tutarsız?
Eğer gerçekten \angle BAC = 40^\circ ve \angle BAC = 3 \angle ACB ise bu, \angle ACB = \frac{40^\circ}{3} = 13.\overline{3}^\circ anlamına gelir. Diğer yandan \angle ABC = 36^\circ verilmiş. Bu üç açıyı toplarsak:
Oysa bir üçgende iç açılar toplamı 180° olmak zorundadır. 89.3° civarında bir toplam, 180°’ye eşit değildir. Dolayısıyla metin olduğu gibi doğru okunmuşsa, bu veriler bir üçgenden bahsetmek için çelişkilidir.
4.3. Metindeki Muhtemel Yazım Hataları
- “40°” ifadesi aslında \angle BAC - \angle ACB = 40° gibi bir fark olabilir.
- Ya da \angle BAC = 3 \angle ACB ifadesiyle 40°’ye ayrı bir vurgu yapılıyor olabilir.
- 36^\circ yerine 56°, 46° vb. diğer değerler olabilirdi.
Soruda bir yazım hatası yoksa ve tam bu verilere sadık kalmak gerekiyorsa, normalde bu sorunun “geçersiz” hale geldiğini söyleyebiliriz. Çünkü üçgenin açıları 180° olması gerekir.
4.4. Olası Bir Düzeltilmiş Senaryo
Diyelim ki metin şöyle olmalıydı: “$m(\angle BAC) - m(\angle ACB) = 40^\circ$ ve m(\angle BAC) = 3 m(\angle ACB), ayrıca m(\angle ABC) = 36^\circ.”
Bu durumda işlemler şöyle giderdi:
- \angle BAC = 3c ve \angle ACB = c (burada c bir semboldür).
- Farkları 40° ise: 3c - c = 40^\circ \implies 2c = 40^\circ \implies c = 20^\circ.
- O halde: \angle BAC = 3c = 60^\circ.
- \angle ABC = 36^\circ verildiğinden, toplam: 60^\circ + 36^\circ + 20^\circ = 116^\circ, yine 180° etmez. Bu da tutarsız kalır.
Benzer şekilde farklı tahminler de çelişkiyi çözmemektedir. Bundan dolayı, 4. sorunun çözümü için elimizdeki verilerde bir hata olduğu kanaati güçlenmektedir.
Dolayısıyla Soru (4)’te belirtilen bu sayılarla geçerli bir üçgen oluşturmak mümkün görünmemektedir. Eğer metin başka bir bilgi içeriyorsa veya “= 40°” ifadesi başka bir açıyı tanımlayıp sizde eksik kaldıysa, soruyu düzeltmek gerekebilir.
SORU (5): “m(EDC) = 110°, m(DEC) = 40°, m(B) = 65°, Buna göre m(BAC) kaç derecedir?”
Sorunun görselinde, ABC üçgenine ek olarak bir D ve E noktası görülüyor. Metin kısmen şunları söylüyor:
- “ABC bir üçgen”
- m(\angle EDC) = 110^\circ
- m(\angle DEC) = 40^\circ
- m(\angle B) = 65^\circ (yani \angle ABC = 65^\circ)
Ve “Buna göre m(\angle BAC) kaç derecedir?” sorusu var.
Burada E ve D noktalarının üçgende veya uzantılarında nasıl konumlandığı belirsiz; “E” ile “D” bir dış üçgen mi oluşturuyorlar, yoksa “E” ve “D” üçgenin içindeki birer nokta mı? Genellikle çizimlerden şu tip bir senaryo olabilir:
- Üçgen ABC
- Bir nokta E, AC kenarı veya AB kenarı üzerinde
- Bir nokta D, BC kenarı veya uzantısı üzerinde
- EDC ifadesi, E–D–C ile oluşturulan bir açıdan bahsediyor.
5.1. m(EDC) = 110°, m(DEC) = 40°
Bu iki açı, EDC üçgeninde ( veya EDC açısı duran bir konfigürasyonda ) yer alıyor olabilir. Fakat m(\angle EDC) + m(\angle DEC) = 110^\circ + 40^\circ =150^\circ. Bu ikisi bir üçgenin iki açısı ise üçüncü açı 30° olur. Tabii bu 30° hangi açıya denk geliyor dersek \angle DCE veya benzer bir gösterim olabilir. Ancak “m(B) = 65°” ifadesi ABC üçgenine aittir.
Eğer bu soruda “E” ve “D” harici noktalarsa, “m(BAC)” ın (yani $\angle A$’nın) kaç derece olduğu farklı geometrik bağıntılardan türetilebilir. Kimi sorularda, “D, BC üzerine alınan bir nokta, E, AB uzantısı vb.” gibi açıklamalar yapılır ve iç/dış ters açı, dış açı teoremi, benzerlik teoremleri (AA, SAS vb.) kullanılabilir.
Ne yazık ki, tek başına “$m(\angle EDC) = 110^\circ$ ve $m(\angle DEC) = 40^\circ$” bilgisi, \angle B = 65^\circ ile nasıl ilişkileneceği belirsiz olduğundan, $m(\angle BAC)’ı (yani \angle A$) hesaplamak için yeterli veri net olarak görülemiyor. Muhtemelen sorunun orijinalinde:
- E noktasının AB kenarında olup olmadığı,
- D noktasının AC kenarında olup olmadığı,
- Veya ED nin BC ye dik olup olmadığı
gibi ek bilgiler vardır. Bu bilgiler olmadan “m(BAC)” direkt bulunamaz.
Aksi yönde: Bazı geometri sorularında m(\angle EDC), m(\angle DEC) gibi ifadeler harici bir üçgende anlatılır ve “şu açı, bu açıya eşittir” ya da “iki doğru paraleldir”, “bir doğrultu 180° oluşturur” gibi ipuçları eklenir. Fotograftaki tek cümlelik değerlendirme yetersiz kalıyor.
Muhtemel Strateji
- Dış açı teoremi: Bir üçgenin herhangi bir dış açısı, o üçgenin o dış açıya komşu olmayan iki iç açısının toplamına eşittir.
- Benzerlik teoremi: Bir üçgende bir köşeden çizilen yardımcı çizgiler, diğer kenarlara paralelse, birçok açı eşitliği veya açıların orantıları ortaya çıkar.
Yine de veriler eksik ya da açıklama yetersiz olduğundan, 5. sorunun tam çözümüne dair kesin sonuç verilemiyor.
SORU (6): “ABC ve BED üçgen. [AB] ⟂ [ED], m(A) = 40°, m(D) = 15°, Buna göre, m(ACB) = x kaç derecedir?”
Fotoğrafta alt kısımda:
- ABC ve BED üçgenleri çizilmiş.
- [AB] \perp [ED] yazıyor (yani AB ile ED dik).
- m(A) = 40^\circ, m(D) = 15^\circ.
- “Buna göre m(\angle ACB) = x kaç derecedir?” diye soruluyor.
Şekilde “A” tepe noktasında 40° lik bir açı, “D” de başka yerde 15° lik açı var; “E” noktasının nerede olduğu, “B” ve “C” ile hangi bağıntıda durduğu tam göremiyoruz. “F” de resimde geçiyor olabilir. Dolayısıyla yine bütüncül çözüm şu anlama gelir:
- ABC üçgeni (A, B, C köşeleri)
- BED üçgeni (B, E, D köşeleri)
- [AB] ve [ED] dik kesişiyor, dolayısıyla \angle (AB, ED) = 90^\circ.
- m(\angle A) = 40^\circ bir yerde, m(\angle D) = 15^\circ başka yerde.
Çoğu zaman bu tip sorularda, AB bir kenar, ED başka bir kenar veya yüksekliğe benzer şekilde konumlanmış olur. “x = m(\angle ACB)$” isteniyorsa, muhtemelen belli bir benzerlik veya tamamlayıcı/dış açı teoremi devrede olabilir.
Ortak stratejiler:
- Eğer “AB” ile “ED” dik ise bu doğruların oluşturduğu açılar 90°dir.
- “A” ve “D” nin açı ölçüleri verilmiş. Bu açıların hangi üçgen(ler) içinde olduğu, ortak kenarlar, paylaşılan doğrular gibi bilgiler yardımıyla $\angle ACB$’ye ulaşılır. Bazen geometrik eklemler (açıların bütünlenmesi, tümlenmesi, dış açıların toplamı vb.) devreye girer.
Tabii yine çizimi ayrıntılı görmeden veya ek postülatları (örn. BE nin AC ile belirli bir açı yaptığı, ya da $E$’nin “A” noktası ile aynı doğrultuda olduğu) bilmeden net bir sonuç çıkarmak çok zor.
GENEL ADIM ADIM ÇÖZÜM YÖNTEMİ
Fotoğrafta görünen bu üç soruda da eksik veya çelişkili veriler mevcut olduğu için, nasıl bir “genel” yaklaşım izlenebileceğini şu şekilde özetleyebiliriz:
Adım 1 – Sorudaki Şekli Netleştirme
- Verilen üçgen(ler)i düzgün biçimde kâğıda çizin.
- Her köşeyi ve üzerine gelen açı bilgilerini işaretleyin.
- Harf sırasına dikkat edin (örn. m(\angle BAC), A’nın tepe açısıdır).
- Noktaların hangi kenarlar üzerinde veya uzantılarında olduğundan emin olun (D, E, F gibi).
Adım 2 – Verileri Listeleyin
- Her açıya dair verilenler: “$m(\angle ABC) = …^\circ$”, “$m(\angle EDC) = …^\circ$” vb.
- Elde ettiğiniz her denklemi yazın (örn. “$m(\angle BAC) = 3 m(\angle ACB)$” ).
- Diklik veya paralellik gibi ek şartları bir yere not edin (örn. “[AB] ⟂ [ED]” demek \angle (AB, ED) = 90^\circ).
Adım 3 – Üçgen Açıları Toplamı (180°)
- Eğer ABC üçgenine ait üç açıya dair bir bağlantı varsa, m(\angle A) + m(\angle B) + m(\angle C) = 180^\circ kuralını kullanın.
- Dış açı teoremi: Örneğin “$m(\angle ACD)$, ABC üçgeninin dış açısı ise, $m(\angle ACD) = m(\angle A) + m(\angle B)$” gibi kurallardan faydalanın.
Adım 4 – Benzerlik, Açı-Açı (AA) Eşliği, Üçgenlerin Ortak Açıları
- İki üçgenin belirli kenar veya açı ilişkileri varsa, benzerlik (AA) yardımıyla açı ölçüleri arasında eşitlik kurabilirsiniz.
- Özellikle “m(A) = 40°, m(D) = 15°” gibi bilgiler bazen benzer üçgen çiftlerinde paylaşılan açıların yardımıyla x in bulunmasını sağlar.
Adım 5 – Sonucu Kontrol Edin
- Elde ettiğiniz açı değerlerini her zaman 180°lik kural ile kontrol edin.
- Bir üçgenin açıları toplamı 180°’yi geçiyorsa veya altındaysa, verilerde hata olduğunu ya da ek bir geometrik bilginin eksik olduğunu tespit etmiş olursunuz.
ÖZET TABLO
Aşağıda, fotoğrafta görülen 4, 5 ve 6. soruların durumunu ve hangi verilerin eksik/tutarsız olduğunu özetleyen bir tablo hazırlanmıştır:
| Soru No | Verilen Bilgiler | Muhtemel Amaç | Tutarlılık/Uygulanabilirlik |
|---|---|---|---|
| 4 | m(BAC) = 3m(ACB) = 40°, m(ABC) = 36° (ABC üçgen) | m(BAC) kaç°? | Verilen sayılar bir üçgen için ilerlediğimizde toplam 89.3° gibi oluyor, 180° değil. Dolayısıyla veriler çelişkili veya eksik. |
| 5 | ABC üçgeni, m(EDC)=110°, m(DEC)=40°, m(B)=65° | m(BAC) kaç°? | E ve D noktalarının konumu anlaşılırsa ek açı bağıntıları kurulabilir. Ancak mevcut bilgilendirmede açı hesapları belirsiz ve tek başına yetersiz. |
| 6 | ABC ve BED üçgen, [AB] ⟂ [ED], m(A)=40°, m(D)=15° → x= m(ACB)=? | x değerini (AÇB açısı) bulmak | Şekil net görülmediğinden, nasıl bir diklik ve hangi nokta nerede gibi vardır. Veriler muhtemelen benzerlik/dış açı vb. kurallarla çözüm gerektirir; eksik veri var. |
SONUÇ VE DEĞERLENDİRME
-
Soru (4)
- m(BAC) = 3m(ACB) = 40°, m(ABC)=36° ifadesiyle doğrudan çözersek, üçgenin iç açıları 180°’ye ulaşmıyor. Bu gösteriyor ki problem ifadesinde muhtemel bir hata var. Dolayısıyla soruyu o haliyle çözmek olanaksız.
-
Soru (5)
- m(\angle EDC) ve m(\angle DEC) açıları, dışta veya bir yardımcı üçgenin içinde olabilir. “$m(\angle B) = 65^\circ$” ifadesi de üçgen ABC’ye yöneliktir. Fakat $m(\angle BAC)$’a ulaşabilmek için hangi açılar birbirine eş veya hangi çizgiler paralel/dik gibi daha fazla bilgiye ihtiyacımız var.
-
Soru (6)
- [AB] \perp [ED] koşulu, m(\angle A) = 40^\circ ve m(\angle D) = 15^\circ gibi veriler geometrik bir bağıntıya işaret ediyor olabilir. Ancak “m(\angle ACB) = x” ifadesini kesin bulmak için yine daha kapsamlı bir açıklamaya ihtiyaç var.
Dolayısıyla, fotoğraftaki bilgiler (özellikle 4. soruda bariz çelişki içerdiğinden ve 5-6. soruların çizim detayı eksik kaldığından) şu an eksik veya hatalı görünüyor. Sadece bu verilere bakarak angle (BAC), angle (ACB) vb. tam sayısal sonuçlara ulaşmak mümkün değildir. İlgili soruları orijinal kaynak metninden veya ek çizim açıklamalarından incelemek, eksik parçaları gidermek gerekir.
Kısa Özet:
- (4) numaralı sorudaki sayı kombinasyonu bir üçgenin açılarını vermiyor; bu nedenle çözümsüz.
- (5) ve (6) numaralı sorular içinse şemanın daha açık verilmesi şart. İç/dış açılar, paralellik, benzerlik veya diğer detaylar olmadan sonuca varılamaz.