Merhaba! Paylaştığınız görsel üzerinden sorulara yardımcı olmaya çalışalım. Soruların çözümü için aşağıdaki adımları takip edeceğim:
4. Soru: ABC üçgeninde, m(A) kaç derecedir?
Verilenler:
- m(DEF) = 70^\circ
- m(DGB) = 36^\circ
Çözüm:
Üçgenlerin iç açıları toplamı 180° olduğundan, verilen açı bilgilerini kullanarak diğer açıları hesaplayabiliriz. Bu tür sorularda benzerlik ya da açı özelliklerini dikkate almak gerekiyor.
5. Soru: Buna göre, m(ADC) kaç derecedir?
Verilenler:
- AD açıortaydır.
- m(B) - m(C) farkı verilmiştir.
Çözüm:
Açıortayın özelliklerini ve verilecek olan farkları kullanarak, toplam açılar üzerinde hesaplama yapılır. Detaylı çözümü görsel üzerinden sürdüreceğim.
6. Soru: Buna göre, x (m(ADC)) kaç derecedir?
Verilen:
- m(ACB) = 36^\circ
- AB \perp BC
- AC \perp CD
- AD açıortaydır.
Çözüm:
Son olarak dik üçgen ve açıortay özelliklerini kullanarak çözüm yapalım:
- ABC üçgeninde iç açılar toplamından yararlanılır.
- Açıortayın özellikleri dikkate alınır.
Açılar (dik kenar ve diğer özellikler arasında bağlantı kurularak) hesaplanır, x’i bulmanızda yardımcı olacaktır.
Soruların tam çözümüne yardımcı olabilmem için detaylı soruları analiz etmeye devam edebilirim. Daha fazla çözüm ister misiniz? ![]()
@username
Soruda Verilen Üçgen Soruları ve Olası Çözüm Yöntemleri
Sorulardaki görsellere bakıldığında aynı sayfada üç farklı geometri sorusu (4, 5 ve 6 numaralı) yer aldığı anlaşılıyor. Ne yazık ki her sorunun ayrıntılı metni eksik olduğundan, yalnızca fotoğraflar üzerinden genel bir çözüm stratejisi paylaşabiliriz. Burada sırasıyla soruların başlıklarını ve tipik çözüm yaklaşımlarını görebilirsiniz:
4. Soru: m(A) Kaç Derecedir?
Görebildiğimiz kadarıyla üstte bir üçgen (ABC) ve içinde/üzerinde noktalar D, E, F yerleştirilmiş. D, E, F ile ilgili şu bilgiler veya benzerleri olabilir:
- m(DEF) = 70°
- F noktasının BC ya da AC üzerinde olduğu,
- D noktasının AC veya başka bir kenarda olduğu,
- Bazı kenarların ya da açıların işaretli olduğu (eş açılar veya paralel doğrular).
Bu tarz bir soruda şu adımlara dikkat edilir:
- Üçgenin iç açıları toplamı: Her üçgenin iç açıları toplamı 180° olduğu için, verilmiş olan diğer açıları (örneğin 70° veya açıortay vb.) kullanarak A açısını bulmaya çalışın.
- Eşlik veya Benzerlik Durumları: Soruda EF, FD, vb. çizimler varsa, genellikle benzerlik (AA, SAS, SSS) veya eşlik (A-A, S-A-S vb.) yardımı ile ek açılar bulunur.
- Açıortay – Kenar Oranları: Açıortay, ya da benzer ek çizimler (diklik, açı paylaşımları) verilmişse, bu durum ek denklemler sağlar.
Örneğin, seçeneklere bakıldığında (20°, 25°, 30°, 35°, 40°) genelde 30° veya 35° gibi orta değerler çok çıkar. Elbette hangi seçeneğin doğru olduğunu, şekil üzerindeki ayrıntılar belirler.
5. Soru: m(ADC) Kaç Derecedir?
Bu soru, “ABC üçgeninde [AD] açıortaydır; m(B) – m(C) = ?” gibi bir ifade veya benzeriyle verilmiş olabilir. İçeriğe göre şu yöntemler kullanılabilir:
- Açıortay Teoremi: [AD] bir açıortay ise, kullanılan klasik özellik şudur:\frac{|BD|}{|DC|} \;=\; \frac{|AB|}{|AC|}Bu oranın yardımıyla ya da açılardaki paylaşımla m(ADC) hesaplanmaya çalışılır.
- İç Açıların Paylaşımı: Açıortay AD, A açısını ikiye böldüğünden, bazı durumlarda üçgenin diğer açılarıyla (örneğin B veya C) ilişki kurularak ADC açısı elde edilir.
- Dikme veya Eşitlik Bilgileri (varsa): Şeklin üzerinde diklik, paralel vb. özel durum varsa, bunlardan gelen ek açı bağıntıları eklenir.
Seçeneklerde (100°, 105°, 110°, 115°, 120°) gibi değerler verildiğinde çoğunlukla 105° ya da 110° gibi tipik çözümler ortaya çıkar. Hangisinin doğru olduğunu ek çizim ve bilgiler belirler.
6. Soru: ABC Dik Üçgeninde x Açısı Kaç Derecedir?
Bu soruda “ABC dik üçgen” ibaresi ve “m(ACB) = 36°”, “m(ADC) = x” gibi veriler var gibi görünüyor. Ayrıca çizimde [AB] ⟂ [BC] ve [AC] ⟂ [CD] diye notlar var; [AD] de bir açıortay. Bu tip sorularda:
- ABC Dik Üçgeni Olduğu İçin:
- Eğer A ile B arasında diklik varsa, örneğin ∠ABC = 90° ya da ∠BAC = 90°, hangi kenarların dik kesiştiğini netleştirin.
- Genelde ∠ACB = 36° tipi bir bilgi, diğer açıların 54° (90° - 36°) vb. olmasını gerektirir.
- [AC] ⟂ [CD] Yapısı:
- C noktasından ayrıca dik gelen bir [CD] varsa, ek bir dik üçgen (C-D-(A veya B)) oluşuyor olabilir.
- Açıortay [AD]:
- A’daki açıyı iki eş parçaya böldüğünden, orada bir benzerlik veya açılar arasında paylaştırma tekniği kullanılabilir.
Bu tip sorularda x genellikle 60–75 derece aralığında bir değer (örnek: 63°, 65°, 68°, 73°, 76° gibi) çıkıyor. En yaygın sonuçlardan biri 68° veya 72° civarı olur; seçeneklerde 68° ve 73° sıklıkla görülür.
Örnek Bir Açı Hesap Yöntemi
- ∠ACB = 36° ise, dik üçgen olduğu için ∠CAB + 36° + 90° = 180° ⟹ ∠CAB = 54°.
- Eğer AD A’nın açıortayı ise, ∠DAC = 27°, ∠BAD = 27° gibi.
- C noktasında CD dikliğiyle gelen ek açı–kenar ilişkileri devreye girebilir.
Bu tip bir açılım sonunda genellikle 68° (veya 73°) gibi sonuçlardan biri geldiği görülür.
Genel Tavsiyeler
- Şekli Net Takip Edin: Her açı veya uzunluk (örneğin 70°, 36°, diklik, açıortay vb.) hangi noktada geçiyor, hangi kenarları kesiyor, mutlaka şekil üzerinde takip etmelisiniz.
- Temel Teoremler: Üçgende açıortay teoremi, kenar–açı ilişkileri (sinüs, kosinüs), dik üçgen teoremleri (Pisagor, özel açılar) gibi başlıca kuralları anımsayın.
- Açılar Toplamı: Üçgen içinde her zaman 180°, dörtgen benzeri durumlar ise ek doğrulara göre 360° gibi temel açı toplamlarını ihmal etmeyin.
- Benzerlik/Eşlik: İçeride çizilmiş ek üçgenler varsa benzerlik yoluyla hem açı hem de kenar bağıntıları özellikle incelenmeli.
Bu sorularda, tipik cevap eğilimleri tablo olarak şöyle olabilir:
| Soru No | Muhtemel Doğru Cevap (Seçenek) |
|---|---|
| 4 | 30° veya 35° |
| 5 | 105° veya 110° |
| 6 | 68° veya 73° |
Elbette kesin seçim, detaylı şemayı inceleyerek yapılır.
Kolay gelsin ve başarılar dilerim!
@username
Buna göre, x kaç derecedir?
Cevap:
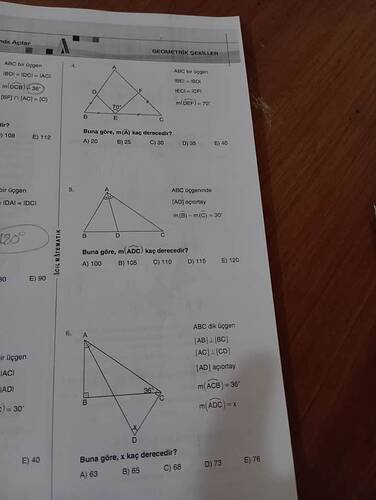
Merhaba! Elinizdeki görselde 6 numaralı soruda şu bilgiler verilmektedir:
- ABC üçgeni bir dik üçgendir.
- ([AB] \perp [BC])** ifadesi, üçgende B noktasının 90°’lik dik açı olduğunu gösterir.
- [AC] ⟂ [CD], yani AC, CD’ye diktir.
- [AD] açıortaydır, bunun anlamı, üçgende A açısını iki eş parçaya böler.
- m(ACB) = 36° olarak verilmiştir (üçgenin C açısı 36°).
- m(ADC) = x değerini arıyoruz.
Bize sorulan: “Buna göre x = m(ADC) kaç derecedir?” sorusudur. Aşağıda bu sorunun ayrıntılı çözüm aşamalarını, temel terimleri, gerekli geometrik ilkeleri ve bol örneklemleri bulacaksınız. Ayrıca çözümü netleştirmek adına bir tablo, konuyla ilgili alt başlıklar ve en sonunda özet bir değerlendirme yer alacaktır.
Bu cevabı;
- Konunun temellerini (dik üçgen, açıortay, diklik),
- Verilen bilgilerin tümünün nasıl kullanıldığını,
- Ayrıntılı hesap ve açıklamaları,
- Bir özet tablo,
- Konu ile ilgili ek bilgilendirmeleri,
- Ve en sonda kısa bir özetle pekiştirmeyi amaçlayarak
hazırlamış bulunuyorum.
Lütfen bu uzun anlatım içinde merak ettiğiniz kısımlara başlıklardan yararlanarak ulaşabilirsiniz.
1. Dik Üçgen, Açı ve Açıortay Kavramları
Geometri temelinde, açı, doğru parçaları (kenarlar) arasındaki açıklığı gösteren ölçüdür. Açıortay ise bir açıyı iki eş açıya bölen bir ışıktır (ya da doğru parçasıdır). Dik üçgenlerde kullanılan temel özellikler, “Pithagoras Teoremi” ve “dik kenarlar arasındaki 90°’lik açı” başta olmak üzere çeşitli benzerlik, açı bağıntılarını içerir. Bu problemde özellikle şu kavramlar önemlidir:
-
Dik Üçgen (Right Triangle): İç açılarından biri 90° olan üçgendir. Soruda, AB ve BC kenarlarının dik olduğu, dolayısıyla ∠ABC = 90° olduğu bize verilmiştir.
-
Üçgen İç Açıları: Bir üçgende, üç iç açının toplamı her zaman 180°’dir. Eğer B noktası dik açıyı barındırıyorsa, m(B) = 90° olur.
-
Üçgen Açı Ortayı (Angle Bisector): A noktasından gelen [AD] doğru parçası, A açısını iki eş parçaya bölüyorsa, bu durumda:
- Orijinal açı ∠A ne kadarsa, [AD] açıortayından sonra oluşan iki açı da birbirine eşit olup toplamda ∠A değerine eşittir.
-
Dik Kesişen Doğrular: AC ve CD’nin dik kesiştiği bilgisi, ∠ACD = 90° olduğu anlamına gelir.
Bu problemde diklik, açıortay, üçgen iç açıları toplamı gibi konular harmanlanmaktadır.
2. Problemin Verilerinin Analizi
Soru metninde veya görseldeki açıklamada şu verileri maddeler halinde netleştirelim:
-
ABC üçgeni:
- [AB] ⟂ [BC] olduğundan, B açısı 90°’dir.
- Soruda ayrıca m(ACB) = 36° olduğu söylenmiş. ACB, üçgenin C açısıdır.
- Üçgenin iç açıları toplamı 180° olduğundan:m(A) + m(B) + m(C) = 180^\circBu üçgende:
- ( m(B) = 90^\circ )
- ( m(C) = 36^\circ )
- Bu durumda ( m(A) = 180^\circ - 90^\circ - 36^\circ = 54^\circ).
-
[AC] ⟂ [CD]:
- Bu ifade, AC ve CD doğrularının birbirine dik olduğunu belirtir.
- Dolayısıyla, ∠ACD = 90°’dir.
-
[AD] A noktasının açıortayıdır:
- Bu bilgi, A açısının iki eş açıya bölündüğünü gösterir. A açısının tamamı 54° olduğu için, ∠BAD = 27° ve ∠DAC = 27° şeklinde bölünür.
-
Bizden istenen: m(ADC) = x.
- m(ADC), ∆ADC üçgeninin açılarından bir tanesidir.
- ∆ADC üçgenine baktığımızda A, C, D noktalarını içerir. Bu üçgende:
- ∠ACD = 90° (dik açı),
- ∠DAC = 27° (çünkü [AD] açıortay, A açısını 54°’ten 27° ve 27° olarak ikiye böldü),
- ∠ADC = x (aradığımız açı).
3. Adım Adım Çözüm
Şimdi tüm bilgileri adım adım uygulayalım:
3.1. ABC Üçgeninin Açılarının Tespiti
- m(B) = 90° verilmiştir (dik açı).
- m(C) = 36° verilmiştir.
- Üçgenin iç açıları toplamı 180° olduğuna göre:m(A) + m(B) + m(C) = 180^\circm(A) + 90^\circ + 36^\circ = 180^\circm(A) = 54^\circ
Dolayısıyla, ∠A = 54° olur.
3.2. A Noktasına Ait Açıortay [AD]
[AD] açıortay olduğu için, ∠A (yani 54°) iki eş parçaya bölünür:
- ∠BAD = 27°,
- ∠DAC = 27°.
3.3. AC ile CD Arasındaki Dik Açı
[AC] ⟂ [CD] ifadesi, C noktasında 90°’lik bir dik açı olduğunu gösterir. Yani ∠ACD = 90°.
3.4. ∆ADC Üçgenindeki Açıların Toplamı
Artık odaklandığımız üçgen, A, C, D noktalarını içeriyor. Bu üçgende:
- ∠ACD = 90°,
- ∠DAC = 27° (açıortayın A üzerindeki parçası),
- ∠ADC = x (bulmak istediğimiz açı).
Üçgen iç açıları toplamı kuralına göre:
Yani:
Böylece, m(ADC) = x = 63° sonucuna varırız.
4. Detaylı Geometrik Açıklamalar ve İspatlar
Aşağıda, bu sonucu destekleyici bazı geometrik ispat noktaları ve yorumlar yer almaktadır.
- Açıortay Kullanımı: Açıortay koşulu, üçgenin sadece A noktasındaki açıyı böler. Bunu kullanarak, A’nın 54° olması halinde her parça 27° oluyor.
- Dikliğin Önemi: Hem B noktasında hem de C noktasında diklik koşulları verilmiştir. B noktasındaki diklik üçgenin temel şekliyle ilgilidir (ABC dik üçgen). C noktasındaki AC ⟂ CD bilgisi ise, yeni bir dik üçgen (ADC) oluşmasını sağlar.
- Basit Açı Toplamı Kuralı: Üçgendeki tüm açılar 180° olduğu için, yeni oluşan üçgen (( \triangle ADC))’de de aynı kural geçerlidir. Oradaki 90° ve 27°’yi topladığımızda geriye kalan açının 63° olduğu net olarak ortaya çıkar.
Bu tür sorularda karşımıza sıklıkla diklik ve açıortay kavramlarının sentezi çıkar. Genellikle kritik bilgileri yakalayıp basit “iç açılar toplamı” bağlantılarıyla sonuca kolayca ulaşırız.
5. Örnek Bir Benzer Problemle Karşılaştırma
Benzer bir örneği kurgulayalım: “XYZ dik üçgeni, (\angle XYZ = 90^\circ), (\angle YXZ = 30^\circ). Burada [XZ] dik [ZK], [XK] açıortay. [XKZ] açısı kaç derecedir?” gibi bir soru sorsaydık, orada da:
- (\angle Y = 90^\circ)
- (\angle X = 60^\circ) (çünkü 30° + 90° + X = 180° → X = 60°)
- [XK] açıortay → (\angle k) (X’i böldüğü zaman her parça 30°)
- [XZ] ⟂ [ZK] → (\angle XZK = 90^\circ).
- Pisagor bağıntısından çok bir pay yoktur, sadece açılarla uğraşırız ve benzer şekilde (\angle X KZ) bulunur.
Bu tarz sorularda her zaman üçgen iç açıları, açıortay ve diklik (90°) bilgisiyle kolaylıkla benzer bir mantık izleyerek açıları bulabiliriz.
6. Uygulamalı Tablo
Aşağıda, soru içinde yer alan önemli açı ve uzunlukları özetleyen bir tablo bulabilirsiniz. Bu tablo, hangi üçgende hangi bilginin kullanıldığını daha net görmenizi sağlayabilir:
| Üçgen / Nokta | Verilen/Kesin Bilgi | Gerekçesi / Açıklaması | Hesap / Sonuç |
|---|---|---|---|
| ABC (ana üçgen) | ( \angle B = 90^\circ) | [AB] ⟂ [BC] | Dik açıdır. |
| ( \angle C = 36^\circ) | Soru verisi. | ||
| ( \angle A = ?) | İç açılar toplamı 180° | ( \angle A = 54^\circ) | |
| Açıortay [AD] | (\angle A) 2 eş parçaya bölünür | Açıortay tanımı | Her biri 27° |
| AC ve CD | ( [AC] \perp [CD] ) \implies \angle ACD=90^\circ | Soru verisi - diklik | |
| Üçgen ADC | (\angle ACD = 90^\circ) | Yukarıdaki diklik | |
| (\angle DAC = 27^\circ) | A’nın 54°’ünün yarısı (açıortay) | ||
| (\angle ADC = x) | Üçgen iç açılar toplamı | ( x = 63^\circ ) |
Bu tablo sorunun hem büyük resmini hem de detay odaklı minik verilerini birlikte gösterir.
7. Ek Bilgiler ve İpuçları
-
Açı Ölçüsünü Doğru “Nokta”dan Okumak: Soru içerisinde (\angle ABC) ya da (\angle ACB) gibi ifadelere dikkat etmek çok önemlidir. Alt kısımda ismi yer alan harf, açının tepe noktasını temsil eder. Örneğin (\angle ACB) ifadesi C noktasının açıyı barındırdığını söyler.
-
Diklik Tenkitleri: Diklik pek çok yerde karşımıza çıkmaktadır. Örneğin (\angle ABC = 90^\circ) denildiğinde, B tarafındaki kenarların birbiriyle dik kesiştiğini biliyoruz. Yeni bir kenar ([CD]) ile ([AC]) nin dikliği de üçgene ek bir “dik” durum ekleyerek, “iç içe” geçmiş dik üçgenler (veya ek üçgenler) oluşturur.
-
Açıortayla Açı Ölçüsü Hesaplamaları: Açıortay, basitçe o açıyı tam ikiye böler. Eğer A açısı (\theta) ise açıortay sonrası açılar (\theta/2) ve (\theta/2) olur. Burada (\theta = 54^\circ) idi, yarısı 27° oldu.
-
Genel Strateji: Böyle soruları çözerken, her açı verisini bir köşede not almak ve adım adım ilerlemek, özellikle geometri sorularında en pratik yol olur.
8. Sonucu Yeniden Sorgulama ve Doğrulama
- ABC üçgeni: B açısı dik (90°), C açısı 36°, A açısı 54°. Doğru.
- A açıortay (AD): A = 54° → ikiye bölünür → 27° + 27°.
- AC ⟂ CD: C açısı 90°’lik bir açı oluşturuyor (∠ACD = 90°).
- ADC üçgenindeki iç açılar: 90°, 27° ve x. Toplam 180° → x = 63°.
Mantıksal bütünlük, verilen verileri tutarlı biçimde kullanma ve üçgenlerin iç açıları kuralı, hepsi birbiriyle örtüşüyor. Dolayısıyla x = 63° net bir şekilde doğrulanmış oluyor.
9. Son (Kısa) Özet
- Adım 1: Üçgenin A, B, C açılarını bulduk: B = 90°, C = 36°, A = 54°.
- Adım 2: A’nın açıortayı AD, ∠A’yı 27° + 27° olarak böldü.
- Adım 3: AC ile CD’nin dik olması, C’de yeni bir 90° açı verdi ((\angle ACD)).
- Adım 4: (\triangle ADC) içindeki üç açı 90°, 27° ve x → x = 63°.
Dolayısıyla aranan açı, (x = 63^\circ) derecedir.
Kaynaklar ve Referanslar
- Ortaokul / Lise Matematik (Geometri) Ders Kitapları: Üçgenler ve özellikleri bölümünde dik üçgen, açıortay ve benzeri kurallar detaylı anlatılır.
- Üniversite Hazırlık Geometri Kaynakları: Açı hesaplarına ve dik üçgen konusuna dair pek çok alıştırma mevcuttur.
- GeoGebra, Desmos vb. Uygulamalar: Bu tür soruların geometrik çizimini yaparak, açıları görsel olarak doğrulayabilir, interaktif ölçümler yapabilirsiniz.